Най-малко общо кратно (НОК)

Здравейте, ученици! Днес ще се запознаем с един важен математически термин – най-малко общо кратно (НОК). Ще разберем какво представлява, как да го намираме и защо е полезен. Ще разгледаме няколко примера и ще решим задачи, за да затвърдим знанията си. Готови ли сте? Да започваме!

1. Какво е най-малко общо кратно (НОК)?

Най-малкото общо кратно на две или повече числа е най-малкото число, което се дели точно на тези числа. С други думи, НОК на няколко числа е най-малкото число, което е кратно на всяко едно от тези числа.

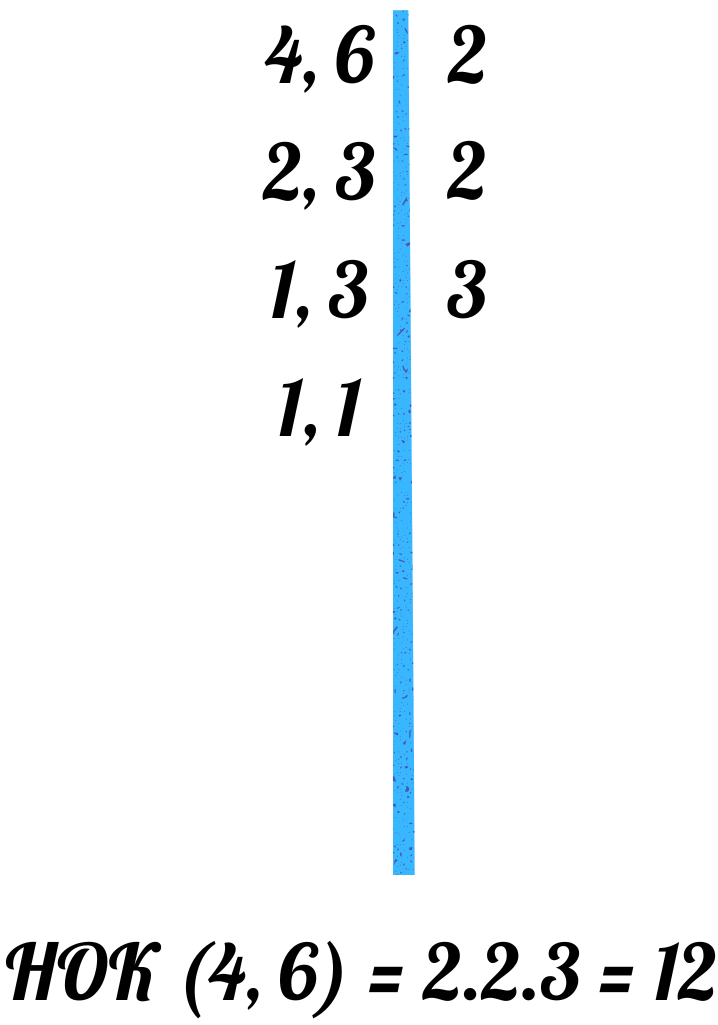
Пример 1: Намерете НОК на 4 и 6

1. Намираме кратните на 4:
   • 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, …
2. Намираме кратните на 6:
   • 6, 12, 18, 24, 30, 36, 42, 48, …
3. Намираме най-малкото общо кратно:
   • Общите кратни на 4 и 6 са: 12, 24, 36, 48, …
   • Най-малкото от тези общи кратни е 12.
   • Значи НОК(4, 6) = 12.
   • Можем да запишем още по следния начин:

Числото a е общо кратно на числата b и c, ако е кратно на b и на c.

2. Как да намерим НОК?

Има няколко метода за намиране на НОК, но ние ще се съсредоточим върху два от тях:

1. Чрез изброяване на кратните (както направихме в примера по-горе).
2. Чрез разлагане на прости множители.

Пример 2: Намиране на НОК чрез разлагане на прости множители:

Нека намерим НОК на 12 и 18.

1. Разлагаме 12 на прости множители:
   • 12 = 2 × 2 × 3 = 2² × 3¹.
2. Разлагаме 18 на прости множители:
   • 18 = 2 × 3 × 3 = 2¹ × 3².
3. Вземаме най-високата степен на всеки прост множител:
   • Най-високите степени са 2² и 3².
4. НОК е произведението на тези множители:
   • НОК(12, 18) = 2² × 3² = 4 × 9 = 36.
5. Можем да запишем този пример по следния начин:

Най-малкото от общите кратни на няколко числа наричаме най-малко общо кратно на тези числа и бележим с НОК.

3. Изчислителни задачи

Задача 1: Намерете НОК на числата 10 и 15.

Задача 2: Намерете НОК на числата 6 и 9.

Задача 3: Намерете НОК на числата 14 и 20.

Задача 4: Намерете НОК на числата 25 и 30.

Задача 5: Намерете НОК на числата 21 и 28.

4. Текстови задачи

Задача 6: Две лампи мигат с различен интервал. Едната лампа мига на всеки 8 секунди, а другата на всеки 12 секунди. На колко секунди двете лампи ще мигнат едновременно?

• Решение:
  • Намираме НОК на 8 и 12.
  • Разлагане на 8: 8 = 2 × 2 × 2 = 2³.
  • Разлагане на 12: 12 = 2 × 2 × 3 = 2² × 3.
  • Най-високите степени са 2³ и 3¹.
  • НОК(8, 12) = 2³ × 3 = 8 × 3 = 24.
  • Отговор: Лампите ще мигнат едновременно на всеки 24 секунди.

Задача 7: В училище, часовете по математика се провеждат на всеки 3 дни, а часовете по физика – на всеки 4 дни. Ако днес и по математика, и по физика има часове, след колко дни отново ще има часове по двата предмета в един и същи ден?

• Решение:
  • Намираме НОК на 3 и 4.
  • Разлагане на 3: 3 = 3¹.
  • Разлагане на 4: 4 = 2 × 2 = 2².
  • Най-високите степени са 3¹ и 2².
  • НОК(3, 4) = 3 × 4 = 12.
  • Отговор: След 12 дни отново ще има часове по математика и физика в един и същи ден.

Задача 8: Три камиона извозват пръст от строителна площадка. Първият се връща на всеки 10 min, вторият – на 20 min, а третият – на 30 min.Ако излизат едновременно сега, след колко минути най-скоро трите камиона ще бъдат отново заедно на площадката?

• Решение:
  • Намираме НОК на 10, 20 и 30.
  • Разлагаме 10 на прости множители: 10 = 2 × 5 = 2¹х 5¹.
  • Разлагаме 20 на прости множители: 20 = 2 × 2 × 5 = 2²х 5¹.
  • Разлагаме 30 на прости множители: 30 = 2 × 3 × 5 = 2¹х 3¹ х 5¹.
  • Най-високите степени са 2², 3¹ и 5¹.
  • НОК(10, 20, 30) = 2 х 2 х 3 × 5 = 60.
  • Отговор: След 60 минути най-скоро ще се срещнат трите камиона на площадката.

5. Отговори

Задача 1:

• Разлагане на 10: 10 = 2 × 5.
• Разлагане на 15: 15 = 3 × 5.
• Най-високите степени са 2¹, 3¹ и 5¹.
• НОК(10, 15) = 2 × 3 × 5 = 30.
• Отговор: НОК(10, 15) = 30.

Задача 2:

• Разлагане на 6: 6 = 2 × 3.
• Разлагане на 9: 9 = 3 × 3 = 3².
• Най-високите степени са 2¹ и 3².
• НОК(6, 9) = 2 × 3² = 2 × 9 = 18.
• Отговор: НОК(6, 9) = 18.

Задача 3:

• Разлагане на 14: 14 = 2 × 7.
• Разлагане на 20: 20 = 2² × 5.
• Най-високите степени са 2², 5¹ и 7¹.
• НОК(14, 20) = 2² × 5 × 7 = 4 × 5 × 7 = 140.
• Отговор: НОК(14, 20) = 140.

Задача 4:

• Разлагане на 25: 25 = 5 × 5 = 5².
• Разлагане на 30: 30 = 2 × 3 × 5.
• Най-високите степени са 2¹, 3¹ и 5².
• НОК(25, 30) = 2 × 3 × 5² = 2 × 3 × 25 = 150.
• Отговор: НОК(25, 30) = 150.

Задача 5:

• Разлагане на 21: 21 = 3 × 7.
• Разлагане на 28: 28 = 2 × 2 × 7 = 2² × 7.
• Най-високите степени са 2², 3¹ и 7¹.
• НОК(21, 28) = 2² × 3 × 7 = 4 × 3 × 7 = 84.
• Отговор: НОК(21, 28) = 84.

6. По-сложни текстови задачи с НОД и НОК

Ако искате да упражните наученото до тук, можете да опитате текстовите задачи отдолу. Можете да си припомните правилата за изчисление на НОД от тази статия:https://matematko.com/%d0%bd%d0%b0%d0%b9-%d0%b3%d0%be%d0%bb%d1%8f%d0%bc-%d0%be%d0%b1%d1%89-%d0%b4%d0%b5%d0%bb%d0%b8%d1%82%d0%b5%d0%bb-%d0%bd%d0%be%d0%b4/

Задача 1: По повод на предстоящ великденски базар децата от 4.а, 4.б и 4.в клас приготвили комплекти с един и същ брой лакомства. Учениците от 4.а клас направили 483 меденки, от 4.б клас – 686 козуначета, а от 4.в клас – 714 кексчета. Като знаете, че броят на сладките в един комплект е възможно най-големият, намерете колко са всички комплекти.

Задача 2: В зоологическата градина на Прага докарали 46 кафяви, 64 черни и 28 бели мечки. Уредникът на зоопарка трябвало да ги разпредели така, че във всяка клетка да броят на мечките от вид да е един и същ. По колко най-малко черни мечки може да има във всяка клетка?

Задача 3: В детска градина “Дъга” всички деца получили еднакви подаръци от дядо Коледа. Във всеки от подаръците били поставени по 123 банана и 82 мандарини. На колко деца са раздадени подаръци? По колко от плодовете има във всеки подарък?

Задача 4: От жп гара тръгват едновременно три влака: един за Пловдив, един за Варна и един за Бъргас. Влакът за Пловдив тръгва на всеки 16 мин., този за Варна – на всеки 10 мин, а влакът за Бургас – на всеки 12 мин. Ако в 13,30 ч. трите влака са потеглили едновременно от спирката, най-рано в колко часа ще потеглят отново влаковете за Пловдив и Варна, а тези за Варна и Бургас?

7. Едновременно намиране на НОК и НОД

Искаш ли да разбереш един комбиниран начин за намиране едновременно на НОК и НОД? Виж картинката долу и проследи обясненията на Математко:

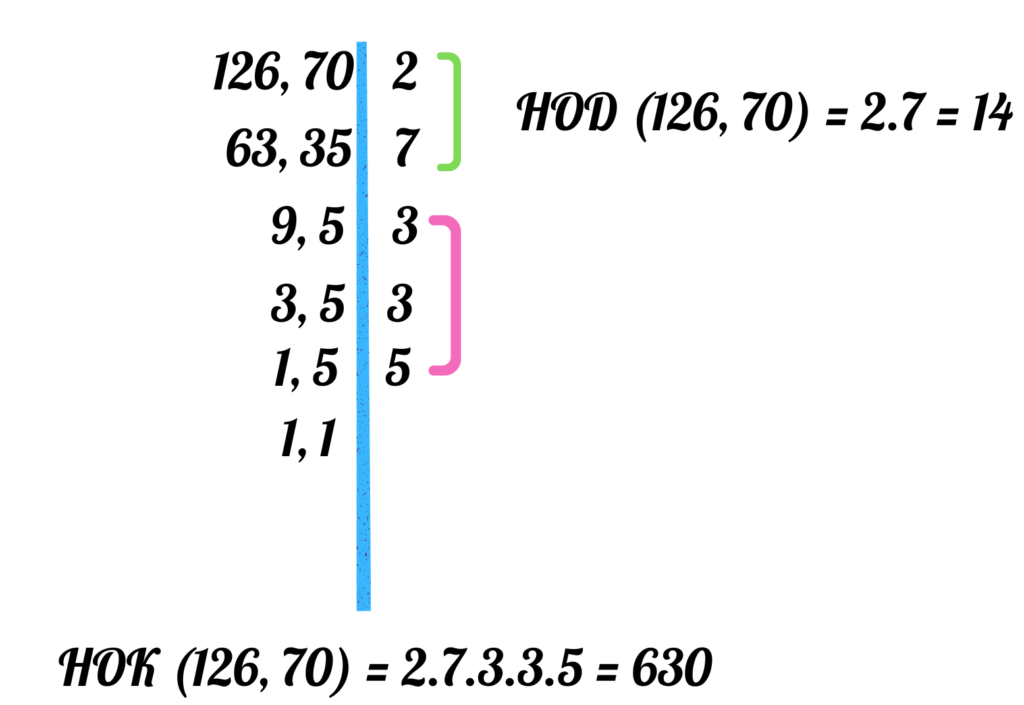
1. Записваме числата едно до друго и поставяме вертикална черта след тях.
2. Намираме общите прости множители на числата. В нашият случай числата 126 и 70 се делят на 2. Записвам го от дясно на линията и извършвам делението.Получените частни записвам отдолу (при нас това са 63 и 35).
3. С частните, които съм получил при делението правя същото. Намирам техния общ прост делител. Тук числата 63 и 35 се делят на 7. Записвам делителя отдясно, а частните на третия ред, долу (след делението се получават 9 и 5).
4. След като съм приключил с общите прости делители, продължавам с делителите на всяко число по отделно. Първо делят 9 на 3.
5. Делението се извършва, докато в ляво на чертата достигна до резултат 1.
6. Математко те съветва, за да не объркаш общите делители, с които изчисляваме НОД, да ги оградиш в кръгче или да ги подчертаеш по подходящ начин!
7. За да намеря НОД, умножавам първите делители, които са били общи за двете числа (тук това са 2 и 7).
8. За да получа НОК, умножавам всички делители, които съм записал от дясно на чертата.

Надяваме се, че тази статия ви помогна да разберете какво е най-малкото общо кратно и как да го намирате. Успех в покоряването на нови математически хоризонти!