Лице на правилен многоъгълник. Лице на съставна фигура.
Здравейте, шестокласници! Време е да се научим да намираме лице на правилен многоъгълник. Днес ще се упражним и с намирането на лице на съставна фигура, но задачите вече ще включват и фигурите кръг и правилен многоъгълник. Да се захващаме за работа!

Ако имате трудности с елементите на правилния многоъгълник, можеш да прочетете статията: Правилен многоъгълник.Елементи.
Лице на правилен многоъгълник
Да разгледаме един правилен шестоъгълник, центърът на който е свързан с всеки от върховете на многоъгълника.
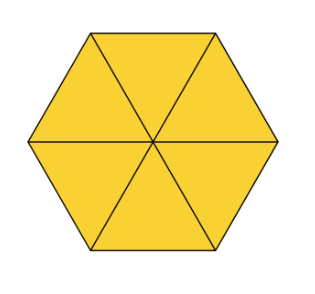
Ако успеем да намерим лицето на единия от всички получени триъгълници, след това ще го умножим по броя на триъгълниците, тъй като те са напълно еднакви.
Лице на триъгълник намираме, като знаем дължините на негова страна и височината към нея. Да разгледаме един такъв триъгълник.
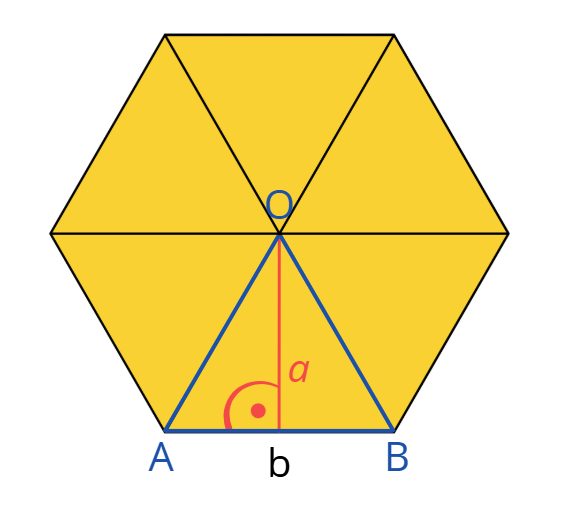
Апотемата на многоъгълника е височина във всеки един от тези еднакви триъгълници.
Лицето му намираме по формулата:
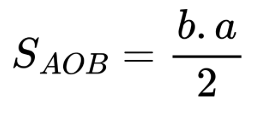
Остава да умножим лицето на триъгълника по броя на триъгълниците. Ами броят на триъгълниците е същият като броят на страните на триъгълника. Получаваме формулата за лице на правилен многоъгълник:
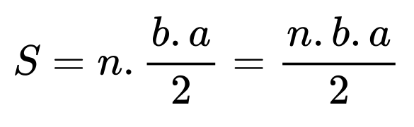
Основни задачи с лице на правилен многоъгълник
Задача №1
Намерете лицето на правилен осмоъгълник със страна 7,2 cm и апотема, която е с 20% по-дълга от страната на многоъгълника.
Дадено:
n = 8
b = 7,2 cm
a = 120%.b
S = ?
Решение:
а = 1,2 . 7, 2 = 8,64 cm
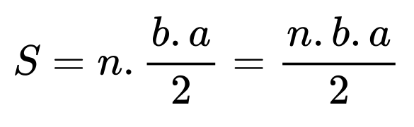
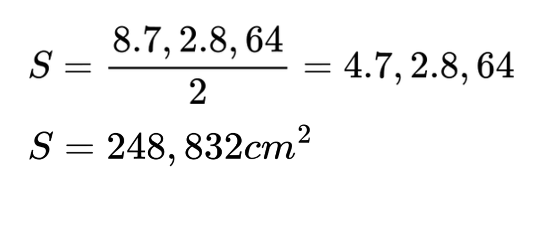
Задача №2
Правилен многоъгълник има лице, равно на 0,216 dm2. Ако страната на многоъгълника е 2,4 cm, a апотемата е с 25% по-къса от нея, намерете какъв вид е многоъгълника.
Дадено:
S = 0,216 dm2
b = 2,4 cm
a = 75% . b = 0,75 . b
n = ?
Решение:
S = 0,216 dm2 = 21,6 cm2
а = 0,75 . 2,4 = 1,8 cm
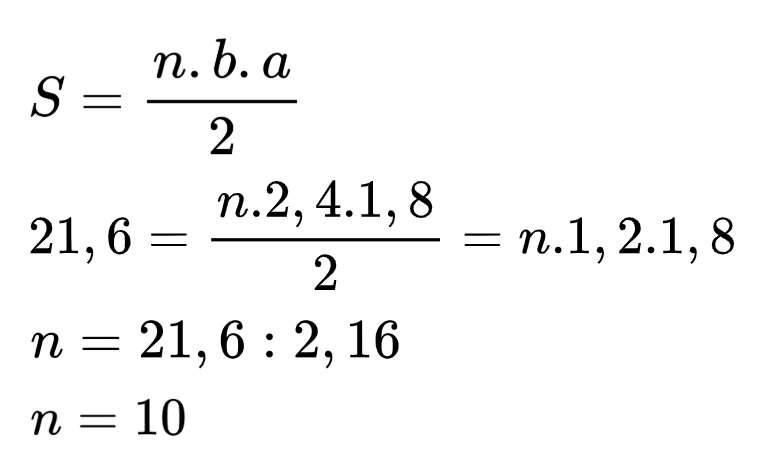
Задача №3
Правилен четириъгълник има лице 49 cm2. Намерете дължината на апотемата на четириъгълника.
Дадено:
n = 4 (фигурата е квадрат)
S = 49 cm2
а = ?
Решение:
Квадратът е правилен четириъгълник. Неговият център съвпада с пресечната точка на диагоналите му, затова апотемата му е разстоянието от тази точка до страната му.
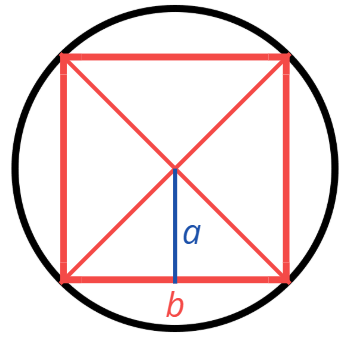
От формулата за лице на квадрат получаваме:
S = b2
49 = b.b
b = 7 cm
Използваме формулата за лице на правилен многоъгълник:
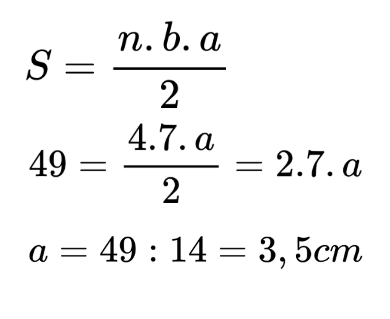
Практическа задача с шевица

Познавате ли богатството на нашите шевици, които украсяват носиите и килимите на предците ни? Най-често шевиците са представлявали комбинация от геометрични фигури. Една от най-популярните наши шевици е канатицата и със сигурност сте я срещали около себе си. Следващата ни задача е с нея!

Върху чипровски килим за изтъкани 100 шевици — “канатица”. Намерете колко квадратни метра е общата площ на шевиците, ако всяка от тях е съставена от 6 броя правилни триъгълници със страна 8 cm и височина приблизително 7 cm.
Решение:
Правилният триъгълник е равностранен триъгълник. Трябва да намерим площта на един такъв триъгълник, да го умножим по 6, за да получим броя на триъгълниците в една канатица и след това по 100, тъй като толкова на брой са всички канатици.
В равностранния триъгълник, освен трите страни, са равни и трите височини към тях. Да намерим лицето на един триъгълник от нашата шевица:
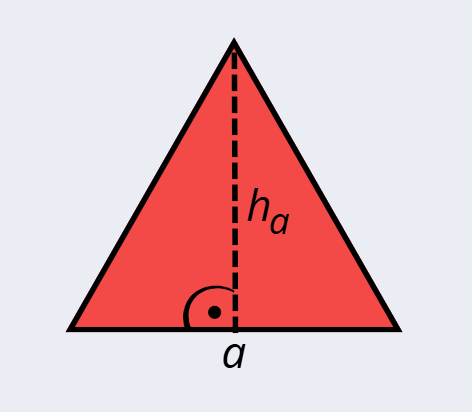
a = 8 cm
ha = 7 cm
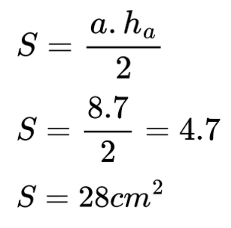
Сега да изчислим площта на всички триъгълници, като вземем предвид, че всяка канатица има 6 такива триъгълника, а броят на всички канатици е 100:
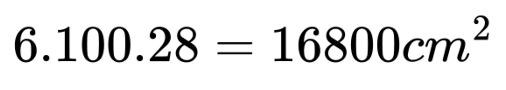
Трябва да запишем площта в квадратни метри. Най-лесно е първо да я пресметнем в квадратни дециметри като разделим на 100 и след това в квадратни метри чрез деление отново на 100. Така преминаваме през съседни мерни единици за площ.

Лице на съставна фигура
Вече са ни познати задачите, в които трябва да намерим лице на фигура, съставена от няколко геометрични фигури. Да разгледаме една подобна задача с новите от шести клас фигури — кръг и многоъгълник.
Намерете лицето на оцветената част от фигурата, като използвате данните от чертежа. Всички дължини са изразени в дециметри.

Решение:
Фигурата е съставена от правилен шестоъгълник и кръг. За да намерим лицето на оцветената част, трябва от лицето на многоъгълника да извадим лицето на кръга.
На чертежа е построена апотемата към една от страните на многоъгълника. Всички страни обаче са с равни дължини, така че имаме всички нужно, за да пресметнем лицето му.
n = 6
b = 12 dm
a = 13,5 dm
S6 = ?
Прилагаме формулата за лице на многоъгълник.
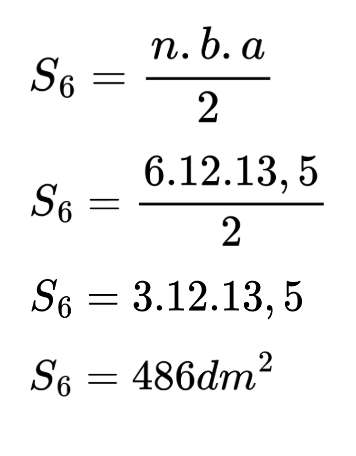
За да намерим лицето на кръга, е достатъчно да знаем неговия радиус. Ако се колебаете дали той е 9dm или 6 dm, запомнете, че надписите по чертежите трябва да се поставят така, че да не сочат надолу. Нашият радиус е 9 dm. Сега да намерим лицето на кръга.
r = 9 dm
S = ?
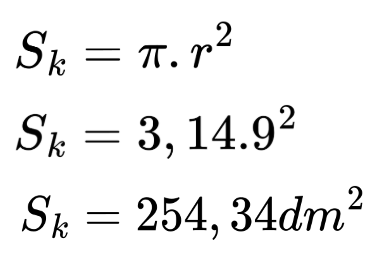
Остава от лицето на многоъгълника да извадим това на кръга.
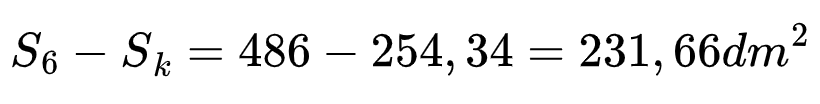

Изгледай следващото видео с още една интересна задача със съставна фигура!
След това се упражни с теста!







