Кълбо. Обем на кълбо.

Кълбо

Планетите от нашата галактика имат формата на кълбо. Това е едно много често срещано тяло в нашата природа. От древни времена учените са го изследвали, а съвременните технологии ни позволяват много прецизно да изчисляваме размерите и обема на различни природни тела с тази форма.

Кълбо можем да получим, когато завъртим полукръг около диаметъра му. Надявам се си спомняте, че за да получим сфера, завъртаме полуокръжност около диаметъра ѝ.

За разликата от сферата, кълбото има обем. Двете тела имат общ център и радиус.

Може да си припомните елементите на сферата ето тук: Сфера.Лице на повърхнина

Елементи на кълбо

Кълбото има следните елементи:

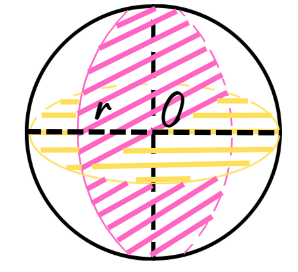
точка О- център на кълбото

r – радиус на кълбото

d – диаметър на кълбото

голям кръг- разделя кълбото на две еднакви полукълба. На чертежа са показани два големи кръга.

Всяка точка от кълбото е на разстояние по-малко или равно от радиуса на кълбото.

Обема на кълбо

Обемът на кълбо се намира по следната формула:

За да намерим обема на едно кълбо, е достатъчно да знаем дължината на неговия радиус.

Вместо думата “обем”, често се използва “вместимост”, особено при течности. Тук трябва да сме много внимателни и с мерните единици за обем и преминаването между тях. За да не допускате грешки е добре да изчислявате съседните мерни единици за обем.

Ако трябва да запишете 2 m³ в mm³, последователно изчисляваме:

2 m³ = (2.1000) dm³ = 2 000 dm³

2 000 dm³ = (2000.1000) cm³ = 2 000 000 cm³

2 000 000 cm³ = (2 000 000.1000) mm³ = 2 000 000 000 mm³

Не забравяйте, обем можем да изчислим на кълбо, но не и на сфера!

Основни задачи с обем на кълбо

Задача №1

Намерете обема на кълбо с диаметър 14 dm и го изразете чрез константата П.

Дадено:

d = 14 dm

V = ?

Решение:

r = d/2

r = 14/2 = 7 dm

V = 4.П.7³/3

V = 1372П/3 dm³

Задача №2

Намерете радиуса на кълбо с обем 36П m³.

Дадено:

V = 36П m³

r = ?

Решение:

36П = 4Пr³/3

Делим двете страни на равенството на константата П и получаваме:

36 = 4r³/3

Умножаваме двете страни на равенството с 3:

108 = 4r³

r³ = 27

r = 3 m

Задача №3

Ива си купила 4 топки сладолед – ментова, ягодова, тирамису и карамел. Намерете обема на всички топки, ако радиусът на топката от мента в сантиметри е равен на най-малкото просто число, ягодовата топка е с обем, който е с 10% по-голям от този на ментовата топка. Топката с вкус на тирамису е с обем, по-голям от тази с вкус на мента с 1/3, а топката карамел е с вместимост с 5% по-малка от тази на ментовата топка. Изчислете обемите с точност до десетите.

Решение:

Най-малкото просто число е 2. Можем да изчислим обема на ментовата топка:

V_мента = 4.3,14.2³/3

V_мента = 33,5 cm³

Сега изчисляваме обема на ягодовата топка.

V_ягода = 110% . V_мента

V_ягода = 1,1 . 33,5 = 36,9 cm³

Топката с тирамису има обем с 1/3 по-голям от този на ментовата топка.

V_{тирамису} = V_мента + 1/3.V_мента

V_{тирамису} = 33,5+ 33,5/3 = 44, 7 cm³

Остава да изчислим обема на топката от карамел.

V_{карамел} = 95%.V_мента

V_{карамел} = 0,95 . 33,5 = 31,8 cm³