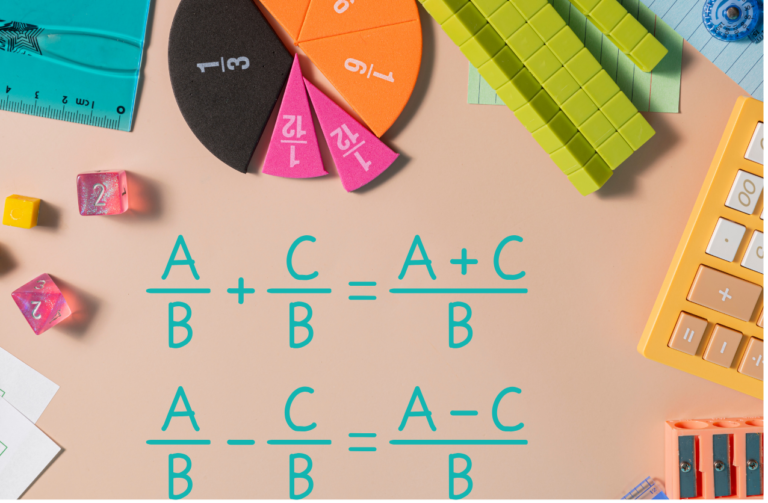Кръг.Лице на кръг.
Здравейте, математици! Време е да се запознаем с геометричната фигура кръг, да се научим да я различаваме от окръжността, както и да намираме лицето ѝ.
Кръг. Елементи на кръг.

Кръгът и окръжността имат много общо елементи. Можеш да си припомниш всичко за окръжността в тази статия: Окръжност.Дължина на окръжност
Много често хората бъркат окръжността и кръга, а те се различават много лесно! Кръгът е образуван от точките на окръжността и всички точки, които се намират вътре в нея (те са на разстояние по-малко от радиуса на окръжността), докато окръжността не включва вътрешните за нея точки.
Да видим кои ще са елементите на кръга:
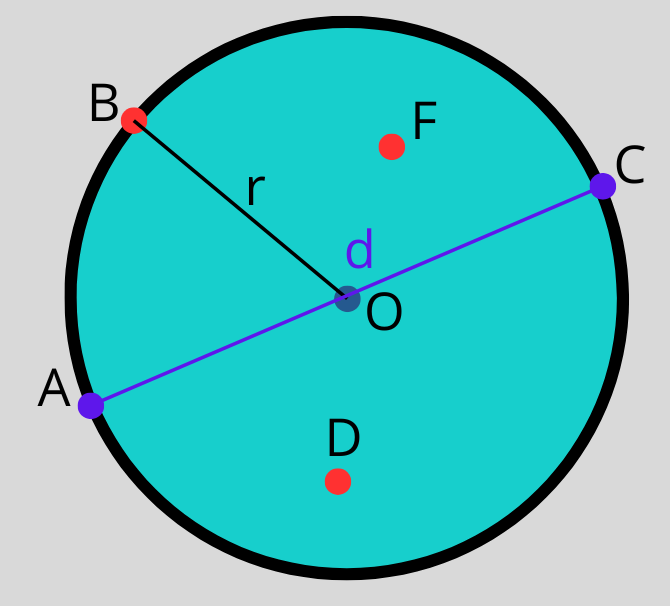
Център на кръга наричаме центъра на окръжността (т.О).
Радиус на кръга наричаме радиуса на окръжността ( OB = r).
Диаметър на кръга наричаме диаметъра на окръжността (АC = d).
Точките D и F са точки от кръга.
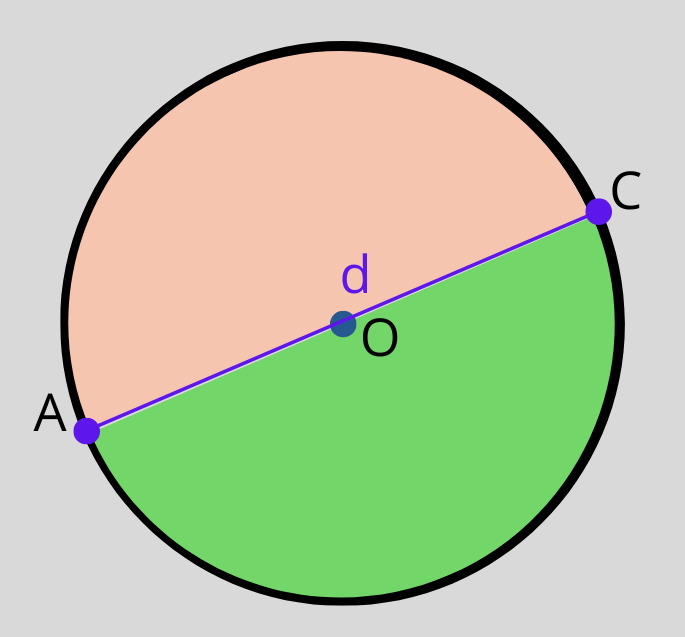
Всеки един диаметър разделя кръгa на две еднакви части, наречени полукръгове.
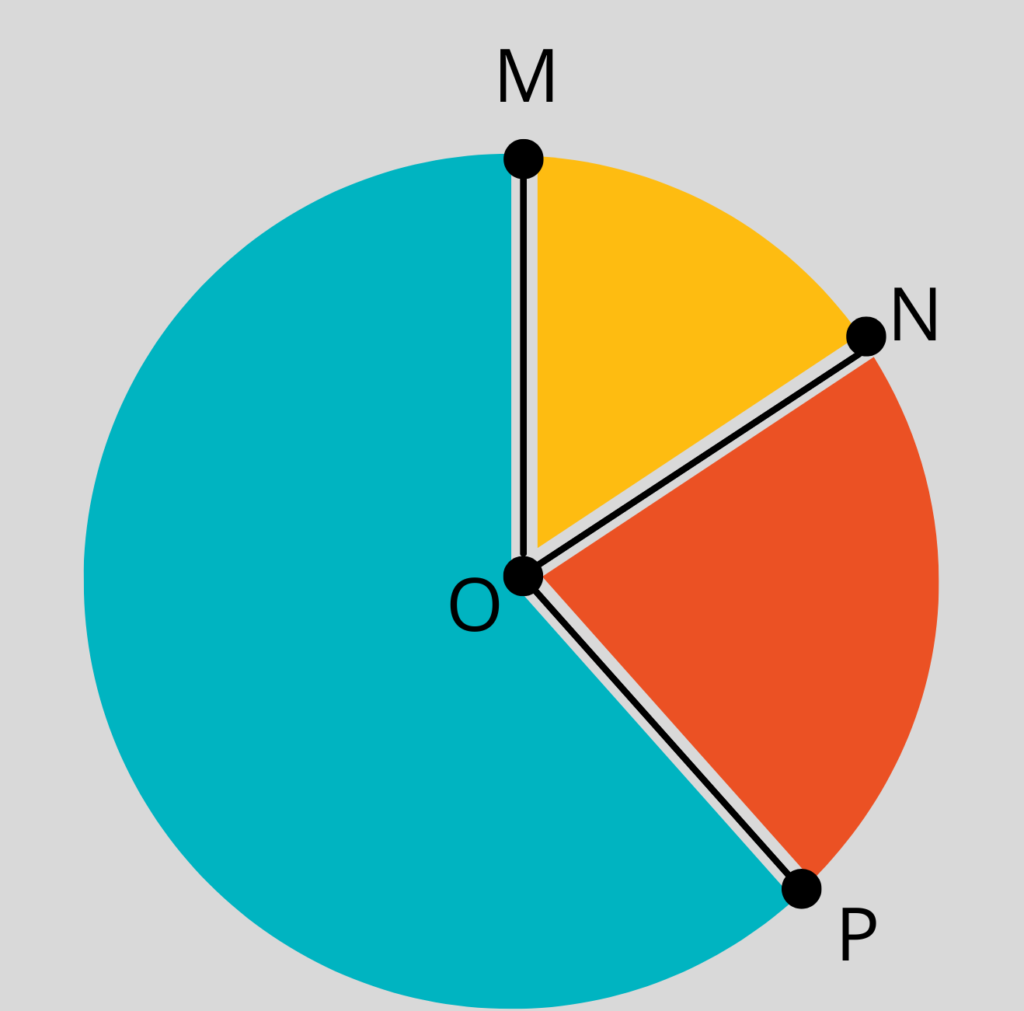
Два радиуса отделят част от кръга, наречена сектор. На нашия чертеж има три сектора — жълт, червен и син.
Ъгълът между два радиуса наричаме централен ъгъл. Такива са ъглите МОN, NOP, MOP. Върхът на всеки един централен ъгъл е център на кръга.
Лице на кръг
Можем да намираме лице на кръг, защото окръжността на кръга загражда площ и точките във вътрешността са част от кръга.

Една от разликите между кръг и окръжност е, че можем да изчислим лице само на кръга! Дължина на окръжността може да се пресмята и за двете фигури.
Има различни начини да се достигне до формулата за лице на кръг. Най-популярни са два от тях. При първия начин се начертава кръг върху квадратна мрежа и започват да се броят целите единични квадратчета, както и тези, които частично принадлежат на кръга, за да се получи приблизителна стойност.

При другия подход кръгът се разделя на сектори с много малък централен ъгъл и след това си представяме, че сме ги подредили плътно един до друг, така че да образуват правоъгълник. Понеже едната страна на правоъгълника е съставена от половината сектори, то нейната дължина е половината от дължината на окръжността на кръга.
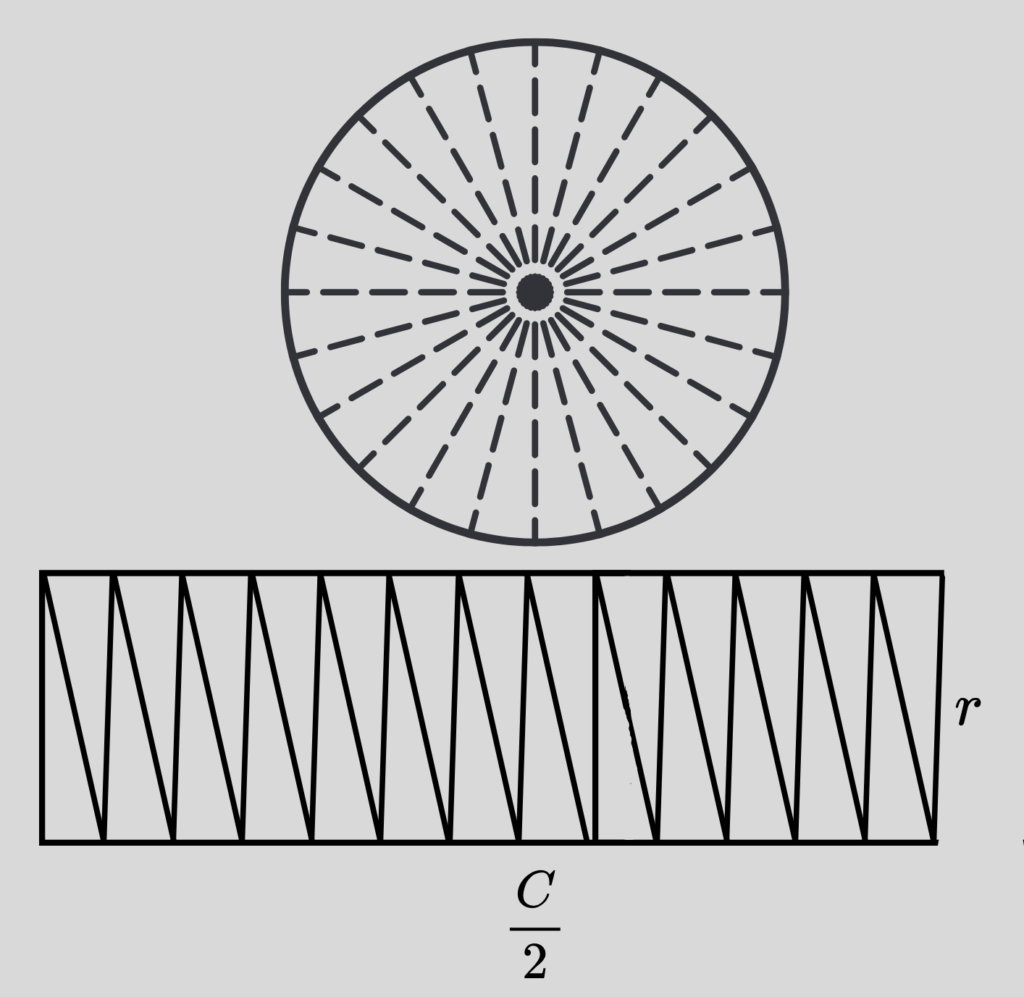
Използваме формулата за лице на правоъгълник, за да изведем лицето на кръга:
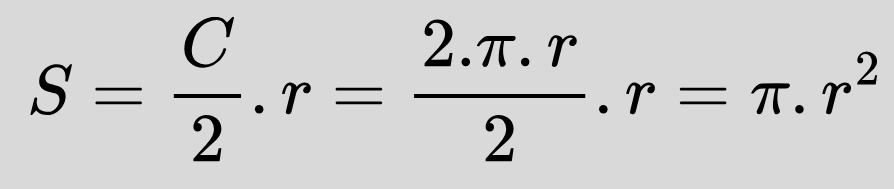
При пресмятането на лице на кръг отново се използва константата П, която може да се замести с обикновена, с десетична дроб или чрез нея да се изрази лицето (не се замества с числова стойност). Запомнете добре тази формула, защото ще ви е нужна и когато изучаваме конус, цилиндър и сфера!
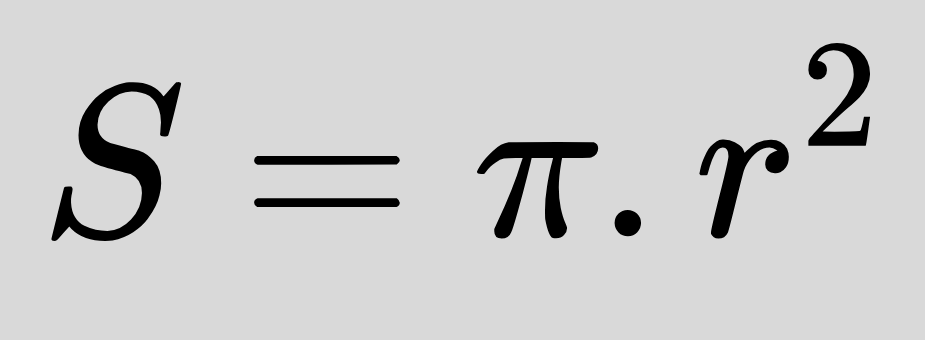
S — лице на кръга
r — радиус на кръга
Основни задачи с лице на кръг
Да разгледаме две основни задачи с лице на кръг:
Задача №1:
Намерете лицето на кръг с диаметър 2,8 cm.

Дадено:
d = 2,8 cm
S = ?
Решение:
Намираме радиуса на кръга, след което го заместваме във формулата за лице на кръг. Константата П ще я заместим с обикновена дроб, както е посочено в условието.
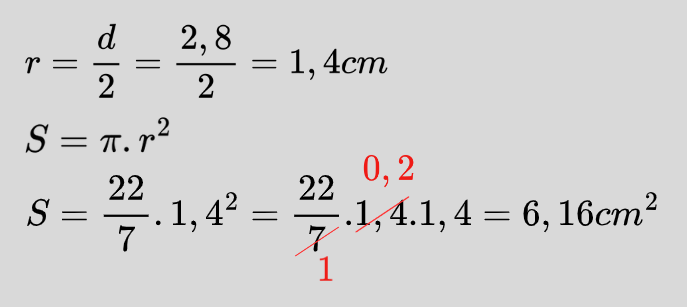
Задача №2:
Лицето на кръг е 9.П dm2. Намерете дължината на окръжността, която го определя.
Дадено:
S = 9.П dm2
C = ?
Решение:
Използваме формулата за лице на кръг, за да намерим неговия радиус.
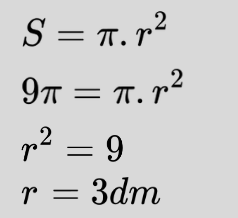
Много е удобно, когато лицето е изразено чрез константата П, тъй като това ни позволява да разделим двете страни на равенството на нея.
Сега остава да намерим дължината на окръжността, която определя кръга:
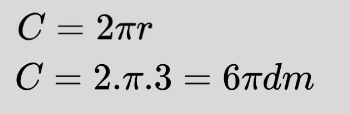
Практическа задача с лице на кръг
За да ушие своята пола, Нина се нуждае от плат. Тя решила, че ще ѝ е нужен кръг с радиус 70 cm, за да получи кройката, която е харесала. Ако си купи плат с размери 1,5 m на 2 m, ще ѝ стигне ли за кройката?
Дадено:
r = 70 cm
Sкр = ?
Sплат = ?
Решение:
Нека първо намерим лицето на кръга, който е нужен за кройката. За целта ще използваме приблизителната стойност на П като десетична дроб и радиуса ще заместим със стойността му в метри. Достатъчно е да закръглим резултата с точност до стотните.
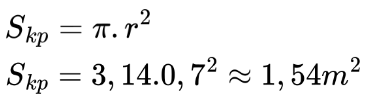
Важно е да направим преценката, че правоъгълникът трябва да е със страни поне 1,4 m, за да може да се изреже кръгът от него.
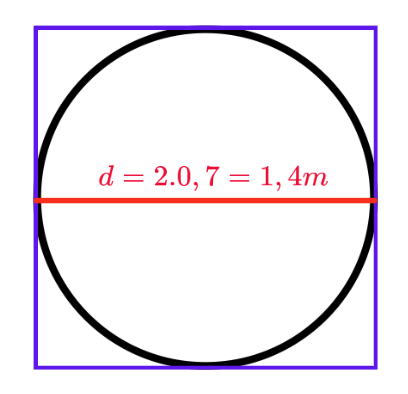
Сега трябва да пресметнем площта на парчето плат, което е с формата на правоъгълник.
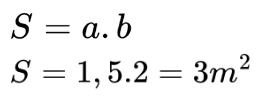
Площта на плата е по-голяма от нужната, така че той ще е достатъчен.
Изгледайте следващото видео, за да разбереш как се намира лице на съставна фигура, когато част от нея е кръг.

Виждате ли колко лесни и приятни са тези задачи?
А сега е време да се упражните със следващия тест!