Задачи със съставни фигури

Най-важното е да си обясним думичката “съставна” фигура. Ами това е фигура, която е съставена от поне две фигури и си нямаме отделна думичка за нея. За да решим задачата, първо трябва да разпознаем фигурите, от които е съставена.

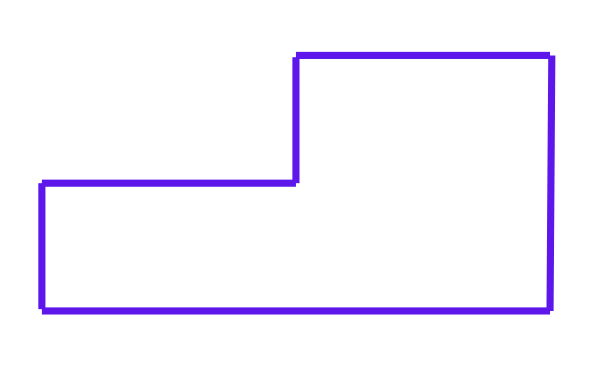
Това е една много простичка съставна фигура, но с нейна помощ ще опишем правилата за намиране на обиколка и лице на съставна фигура.

Тази червена фигура може би ти напомня на парченце от игра за подреждане на пъзел? Тя също ще е наш помощник в днешния урок!

За да е още по-забавно, ще имаме и тази интересна зелена фигура, която има формата на буквата “Н”.

Първата и много важна стъпка е да разделим нашата съставна фигура на такива фигури, които вече познаваме и можем да намираме тяхната обиколка и лице. Колкото по-големи ставате, все повече ще стават фигурите, които познавате и можете да извършвате изчисления с тях.

Ето я и нашата първа фигура! Можем да си представим, че една хоризонтална вътрешна линия я разделя на два правоъгълника.

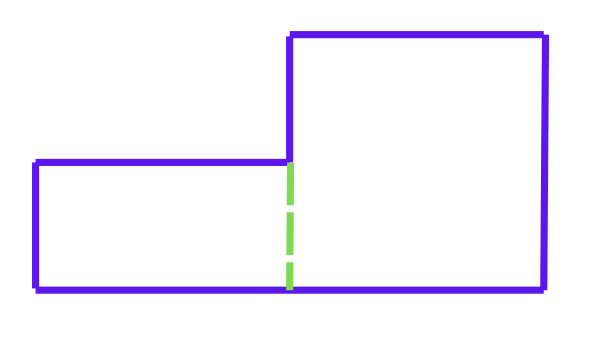
Някой може да реши да раздели фигурата с вътрешна вертикална линия, като така ще получим правоъгълник и квадрат.

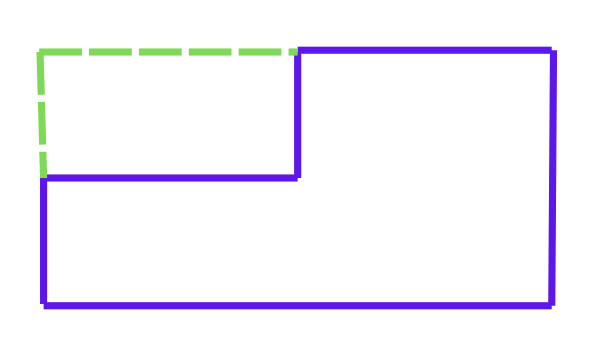
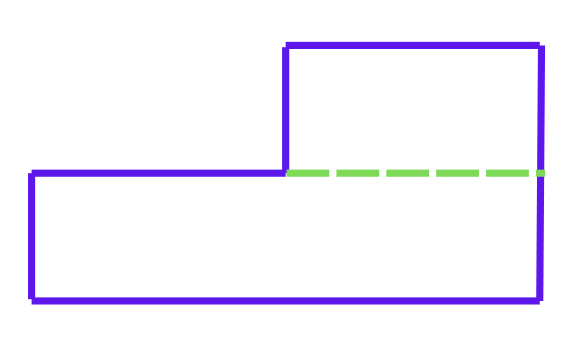
Няма да се изненадам, ако пък си представите, че фигурата се е получила, като от един голям правоъгълник е отрязано парченцето в горния ляв ъгъл! С пунктирна линия е показано как допълваме нашата фигура до един голям правоъгълник.

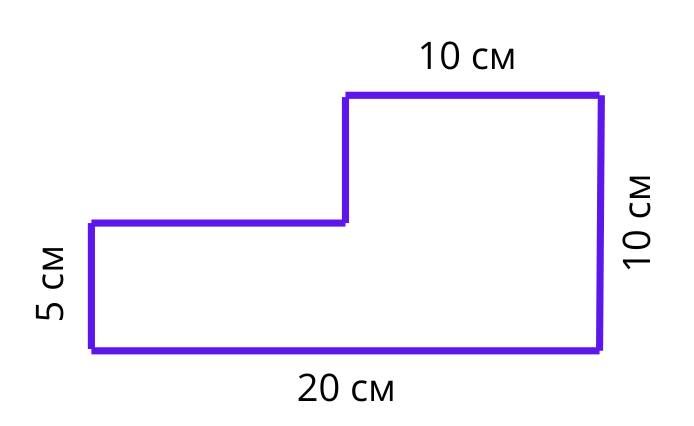
След като ще пресмятаме обиколка на фигура, ще са ни нужни и размери!Това са размерите, които знаем.

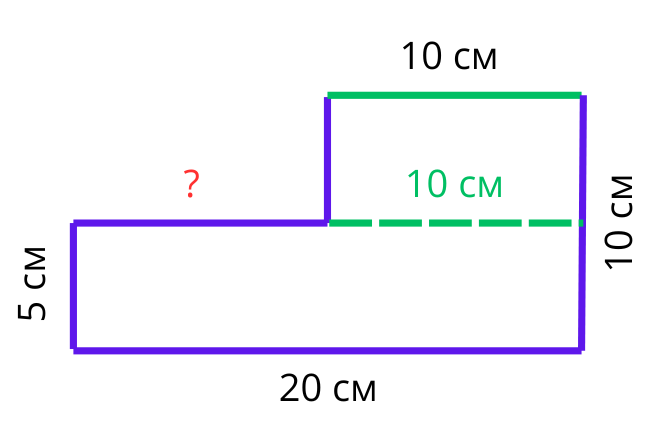
Да открием първо дължината, означена с въпросителен знак. Ако към нея прибавим отсечката, която е равна на означената в зелено 10 см отсечка, ще получим точно 20 см!

Тогава нейната дължина е равна на 20-10=10 см

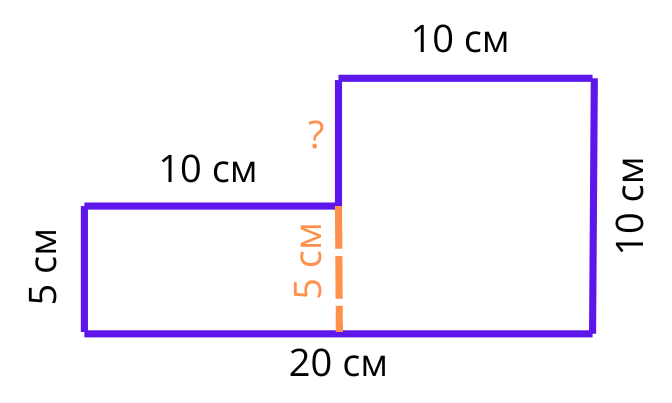
Остана ни само още един размер да изчислим. Тук отново ще си представим, че сме преместили нашата отсечка, дълга 5 см, точно под търсената дължина. Така намираме, че тя е 10-5=5 см.

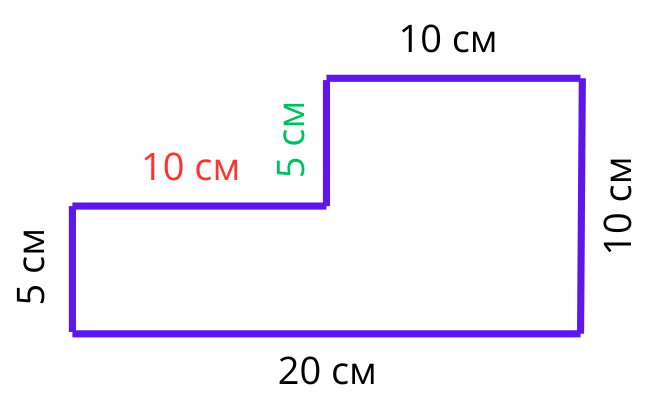
Вече имаме всичко нужно, за да пресметнем нашата обиколка:

P=20+10+10+5+10+5=60 см.

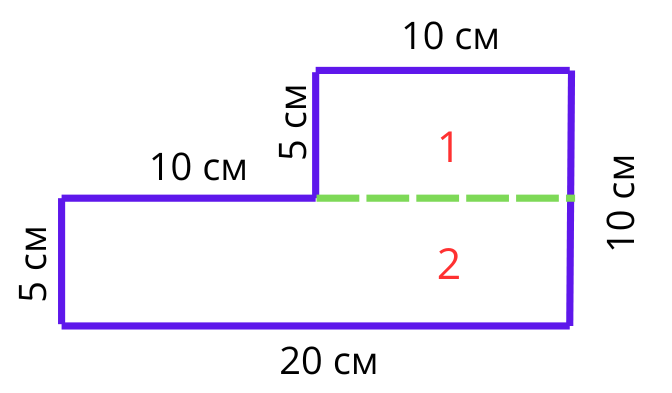
Намираме поотделно лицата на двата правоъгълника, които сме номерирали с числата 1 и 2. За целта използваме формулата за намиране на лице на правоъгълник: S=a.b

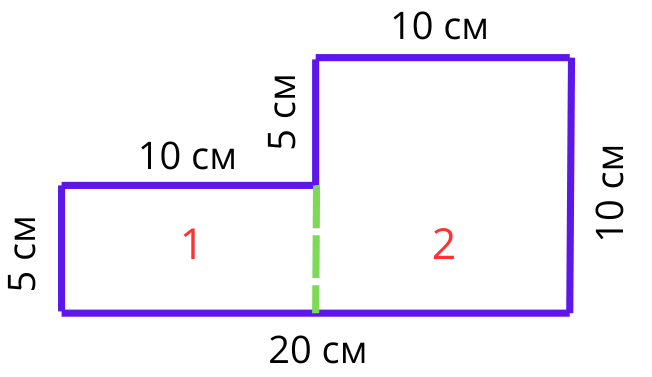
Същата съставна фигура можем да разделим по друг начин, като този път получим един правоъгълник и един квадрат. Да си припомни и формулата за намиране на лице на квадрат: S=a.a

Нека намерим техните лица поотделно и да видим дали ще получим същото лице, когато ги съберем след това.

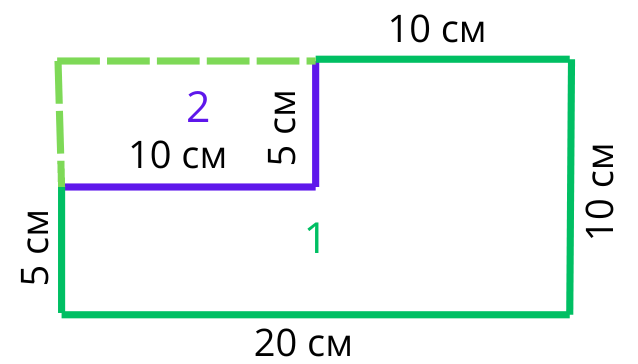
Хайде сега да си представим, че от големият зелен правоъгълник, трябва да отрежем правоъгълникa горе вляво. Тогава лицето на нашата съставна фигура ще е равна на разликата на двете лица.

Получихме едно и също лице на нашата съставна фигура и по трите начина, за които се сетихме да я разделим! Ако пресмятаме правилно лицата на фигурите и сме разделили първоначалната фигура на подходящите фигури, задачата гарантирано е правилно решена!

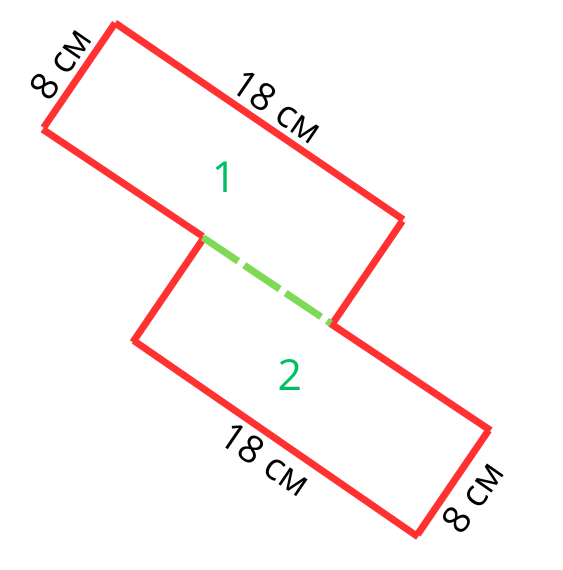
Да се върнем към нашата втора съставна фигура, която прилича на парченце от пъзел! Можем да си представим, че тя е съставена от два еднакви правоъгълника. Ако намерим лицето на единия и го умножеим по две, ще решим задачата.

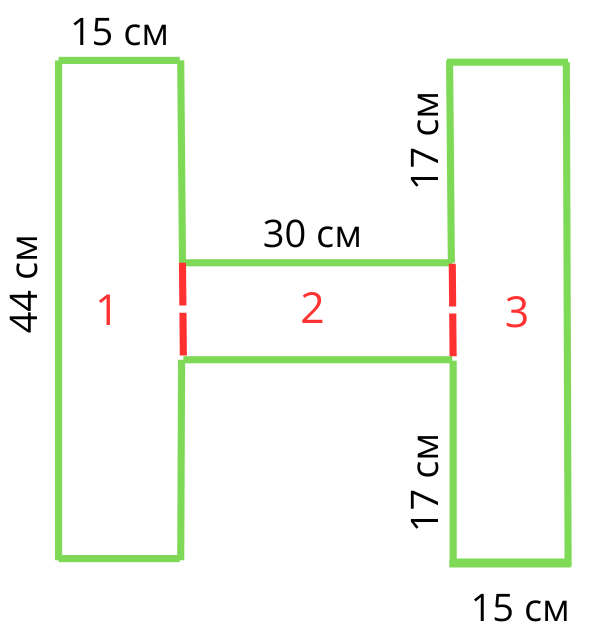
Последната фигура от днешния урок е съставена от три правоъгълника, два от които са еднакви (№1 и №3). Важно е да пресметнем правилно широчината на правоъгълник №2. Тя е равна на 44-2.17=44-34=10 см.

Хайде да пресметнем нейното лице:

Време за още упражнения! Опитай да решиш задачите от теста!