Деление с остатък. Кратно и делител.
Здравейте, приятели! Днес ще поговорим за две важни математически понятия: деление с остатък и какво означават думите “кратно” и “делител”. Ще научим как да делим с остатък и ще видим няколко примера и задачи, за да стане всичко ясно. Готови ли сте? Да започваме!
1. Деление с остатък
Когато делим едно число на друго, не винаги резултатът е точно цяло число. Понякога остава нещо, което наричаме остатък. Например, ако разделим 10 на 3, ще получим 3, защото 3 по 3 е 9, но остава още 1. Това 1 е остатъкът.
Можем да запишем примера по следния начин: 10 : 3 = 3 и остатък 1
Записваме също и така: 10 : 3 = 3 (ост. 1)
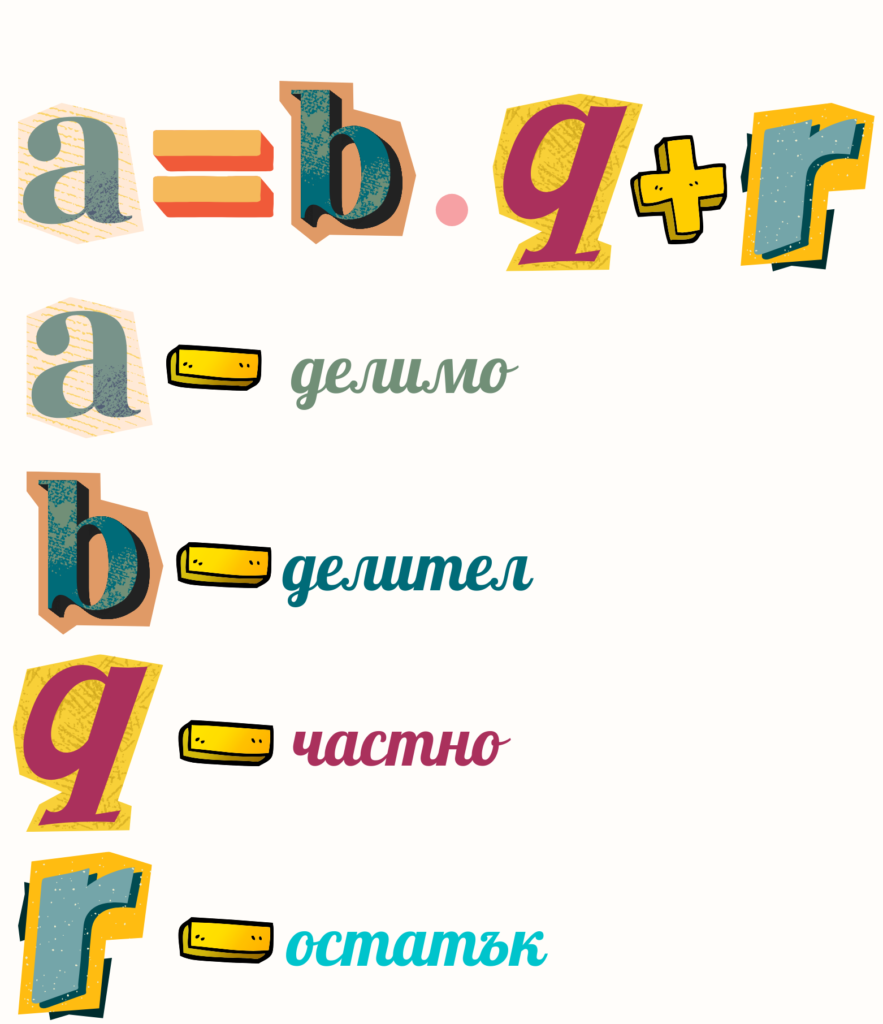
1.1. Стъпки при деление с остатък:
За да направим деление с остатък, трябва да следваме тези стъпки:
- Намираме колко пъти делителят се съдържа в делимото.
- Умножаваме делителя по полученото число.
- Изваждаме полученото произведение от делимото.
Нека видим това с пример:
Разделете 14 на 4.
- Колко пъти 4 се съдържа в 14? Отговорът е 3 пъти, защото 4 . 3 = 12.
- 12 е най-близкото число до 14, което се дели на 4.
- Остава да извадим 12 от 14. Получаваме 2.
Следва, че: 14 : 4 = 3 и остатък 2
Записваме така: 14 : 4 = 3 (ост. 2)
ЗАПОМНИ!
- Делението приключва тогава, когато остатъкът е по-малък от делителя!
- Остатъкът винаги е по-малък от делителя!
- Когато делението е точно, казваме че остатъкът е 0!
2. Кратно и делител
Сега да поговорим за кратни и делители. За целта първо трябва да се научим да разбираме отделните понятия.
Кратно: Когато едно число се дели на друго без остатък, казваме, че първото число е кратно на второто.
Например: 12 е кратно на 3, защото 12 : 3 = 4 без остатък.
Делител: Числото, на което делим, се нарича делител (сигурно си спомняте това от начален етап, където сте учили кои са компонентите на действие деление). В горния пример, 3 е делител на 12.
ЗАПОМНИ!

- Ако остатъкът при деление на числото a на числото b е нула, то числото b се нарича делител на числото a.
- Всяко естествено число се дели на себе си.
- Всяко естествено число се дели на 1.
- Ако остатъкът при деление на числото a на числото b е нула, то числото a се нарича кратно на числото b.
- Всяко естествено число е кратно на себе си.
- Всяко число е кратно на 1.
3. Примерни задачи:
- Пример с деление с остатък: Разделете 17 на 5.
- 5 се съдържа 3 пъти в 17, защото 5 . 3 = 15.
- Остатъкът след изваждане на 15 от 17 е 2.
- Отговор: 17 : 5 = 3 (ост. 2).
2. Пример за кратно: Проверете дали 20 е кратно на 5.
- 20 : 5 = 4 без остатък.
- Значи, 20 е кратно на 5.
3. Пример за делител: Проверете дали 4 е делител на 16.
- 16 : 4 = 4 без остатък.
- Значи, 4 е делител на 16.
4. Задачи за упражнение:
Сега е ваш ред! Опитайте се да решите следните задачи:
- Изчислителни задачи:
- Разделете 23 на 6.
- Разделете 45 на 7.
- Разделете 32 на 8.
- Текстови задачи:
- В една кутия има 29 бонбона. Ако ги раздадем на четири деца, колко бонбона ще получи всяко дете и колко ще останат?

- Петър има 19 молива и иска да ги разпредели поравно на трима свои приятели. Колко молива ще получи всеки приятел и колко ще му останат?

2. Практически задачи:
- Намерете най-голямото число до 50, което е кратно на 7.
- Открийте всички делители на числото 24.
4.1. Отговори на задачите за упражнение:
- Изчислителни задачи:
- 23 : = 3 (ост. 5)
- 45 : 7 = 6 (ост. 3)
- 32 : 8 = 4 (ост. 0)
2. Текстови задачи:
- 29 : 4 = 7 (ост. 1). Всяко дете ще получи 7 бонбона, а ще остане 1 бонбон.
- 19 : 3 = 6 (ост. 1). Всеки приятел ще получи 6 молива и ще остане 1 молив.
3. Практически задачи:
- Най-голямото число до 50, което е кратно на 7, е 49.
- Делители на числото 24 са: 1, 2, 3, 4, 6, 8, 12, 24.
Надяваме се, че ви беше интересно и полезно! Сега знаете какво е деление с остатък и какво означават думите “кратно” и “делител”. Успех в ученето!