Декартова координатна система

Време е за един от най-важните и интересни уроци! Днес ще разгледаме декартова координатна система, ще се научим да определяме координати на точки и да познаваме кои точки са симетрични спрямо осите или началото ѝ.

Координатните системи са нужни, когато трябва да определяме местоположението на обекти в пространството. Те се използват в много приложения, които определят къде се намираме в момента, къде е търсеният от нас адрес или пък пресмятат за колко време ще стигнем до желаното място.

Декартова координатна система

В математиката се използва декартова координатна система, която носи името на своя създател- Рене Декарт. Тя се използва за определяне на местоположение на точки в равнината, за построяване на геометрични фигури, както и за намиране на техните лица. Ето как изглежда:

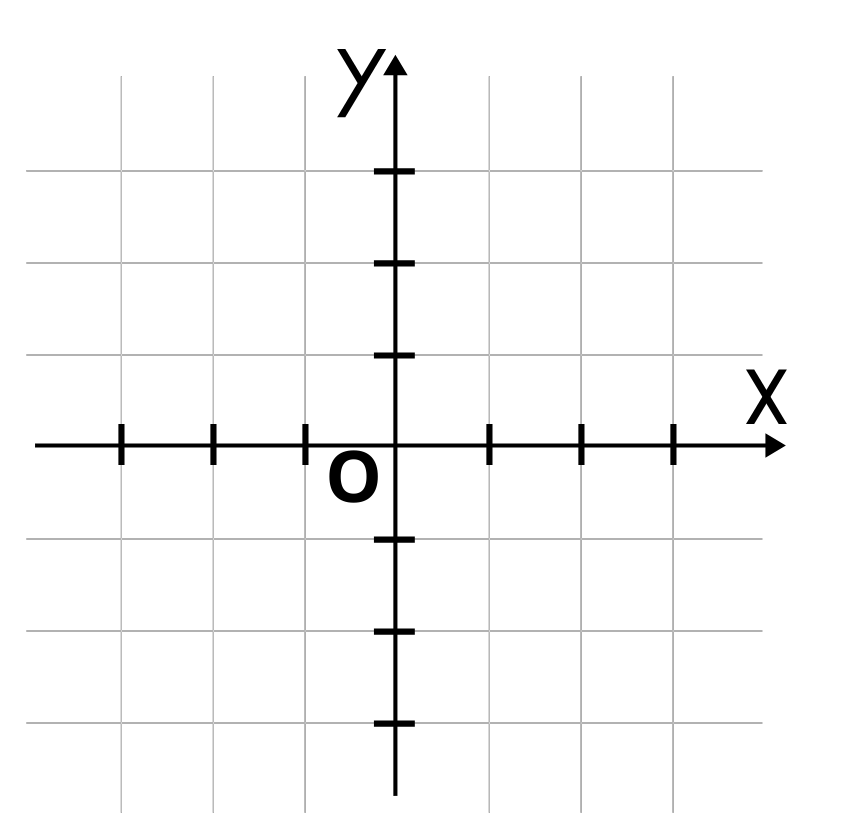
Декартова координатна система се състои от две перпендикулярни оси. Пресечната им точка се нарича начало на координатната система и се означава с О.

Едната ос, хоризонталната, наричаме абсцисна ос. Означава се Оx.

Втората ос, вертикалната, наричаме ординатна ос, означаваме я Оy.

Двете оси са разграфени с една и съща единична отсечка, също както сме свикнали да го правим с числовата ос, когато искаме да изобразяваме на нея рационални числа.

Определяне на координати на точки

По всяка от двете оси нанасяме еднакви единични отсечки като започваме от координатното начало, което съвпада с числото 0. Абсцисната ос разграфяваме точно, както сме свикнали- надясно от нулата са положителните числа, а наляво- отрицателните. Положителните числа при ординатната ос са нагоре от координатното начало, а отрицателното-надолу. Нека да ги видим:

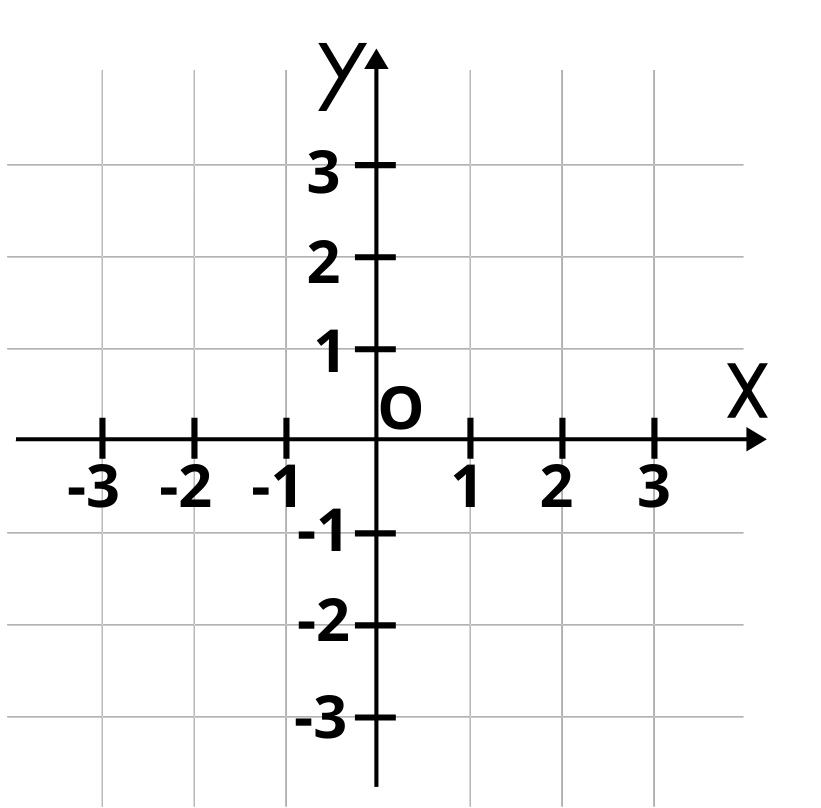
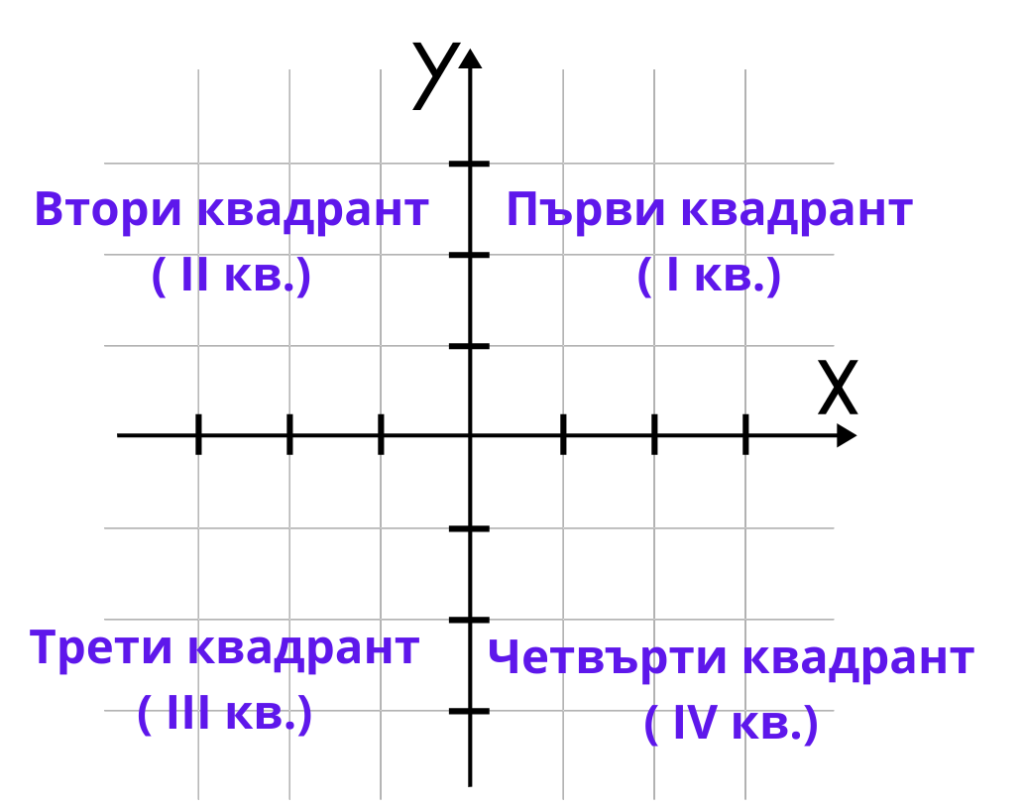
Двете оси на декартовата координатна система разделят равнината на четири части, които се наричат квадранти.

Достатъчно е да запомните къде се намира първи квадрант, следващите се надписват последователно като завъртаме обратно на часовниковата стрелка.

Местоположението на всяка една точка в равнината се определя с две координати- абсциса и ордината, които се записват като наредена двойка числа (x; y).

Винаги първо се записва абсцисата, ако ги разменим, ще получим координатите на друга точка!

Координатното начало е с координати, равни на 0 по двете оси, затова записваме: O (0;0).

Да видим сега как ще определим координатите на точка!

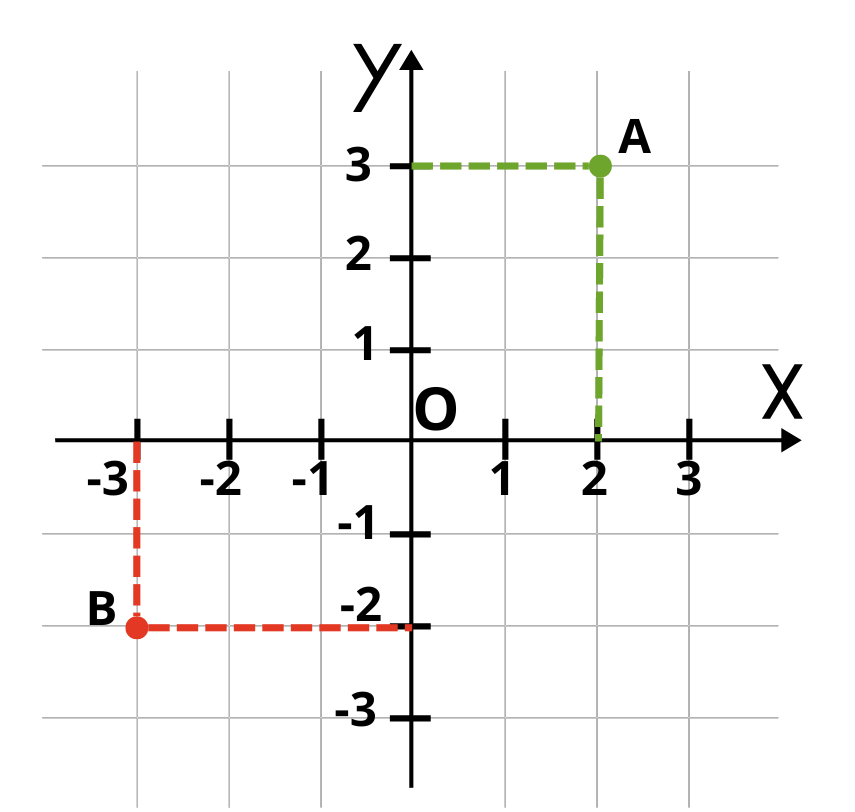
Координатите на всяка една точка в декартова координатна система получаваме като спускаме перпендикуляри към съответната ос и отчитаме стойностите.

След като построим перпендикуляр от точка А до оста Оx, виждаме че отчетът по оста е 2. След това построяваме перпендикуляр от точка А до оста Оy и отчитаме по оста стойност 3. Точка А има абсциса, равна на 2 и ордината, равна на 3. Записваме A(2;3).

По същия начин спускаме перпендикуляри от точка B към абсцисната и ординатната ос. Точката се намира в трети квадрант, затова координатите ѝ са отрицателни числа. Внимаваме при записването на координатите първо да бъде отчетът по оста Оx, а след това по Oy. Записваме B(—3;—2).

Да видим какво се случва, ако имаме точка, която лежи на някоя от двете оси:

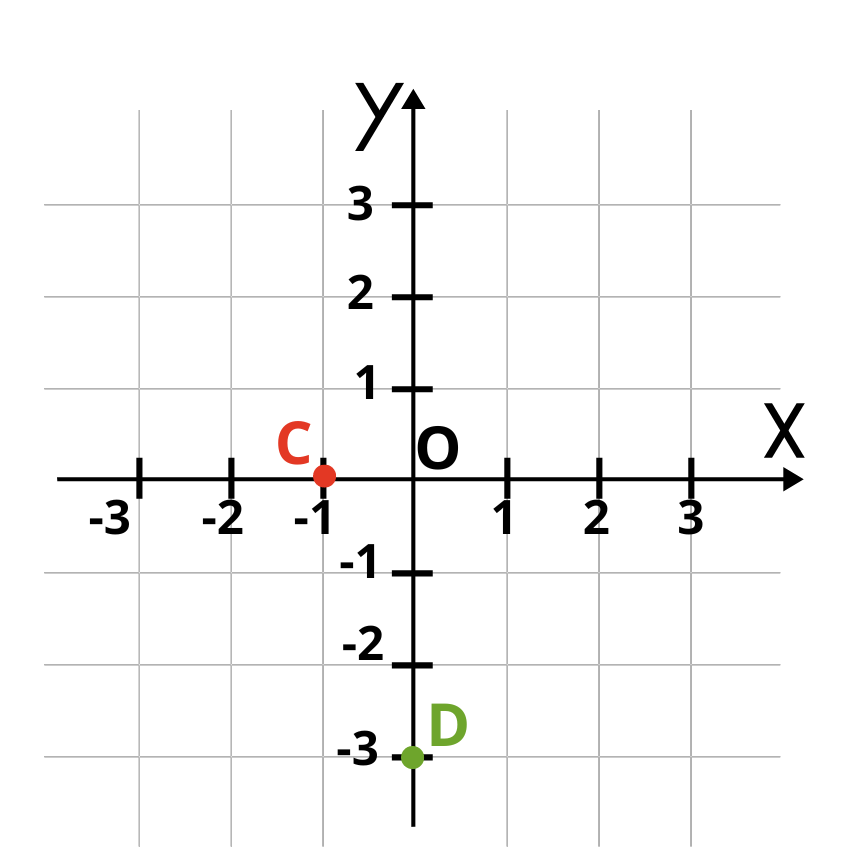
Tочка C лежи на абсцисната ос. Ако спуснем перпендикуляр към ординатната ос, той ще пресече оста точна в началото координатната система или отчетът ще е 0 по оста Oy. Записваме C(—1;0).

Аналогично, ако спуснем перпендикуляр от точка D до абсцисната ос ще попаднем в координатното начало. Затова тя ще бъде с координати D (0; —3).

Ако дадена точка лежи на оста Оx, то нейната ордината ще е равна на 0.

Ако дадена точка лежи на оста Оy, то нейната абсциса ще е равна на 0.

Построяване на симетрични точки на дадена точка.

Много често в задачите с координатна система се изисква да построим симетрична точка на дадена точка. Имаме три варианта на симетрия при декартовата координатна система:

симетрия спрямо абсцисната ос
симетрия спрямо ординатната ос
симетрия спрямо координатното начало

Когато трябва да построим симетрична точка на дадена точка спрямо абсцисната ос, то тя трябва да се намира на същото разстояние от оста Ox като дадената точка. Симетричната точка ще има същата абсциса, но ординатата ѝ ще е противоположно число на ординатата на дадената точка:

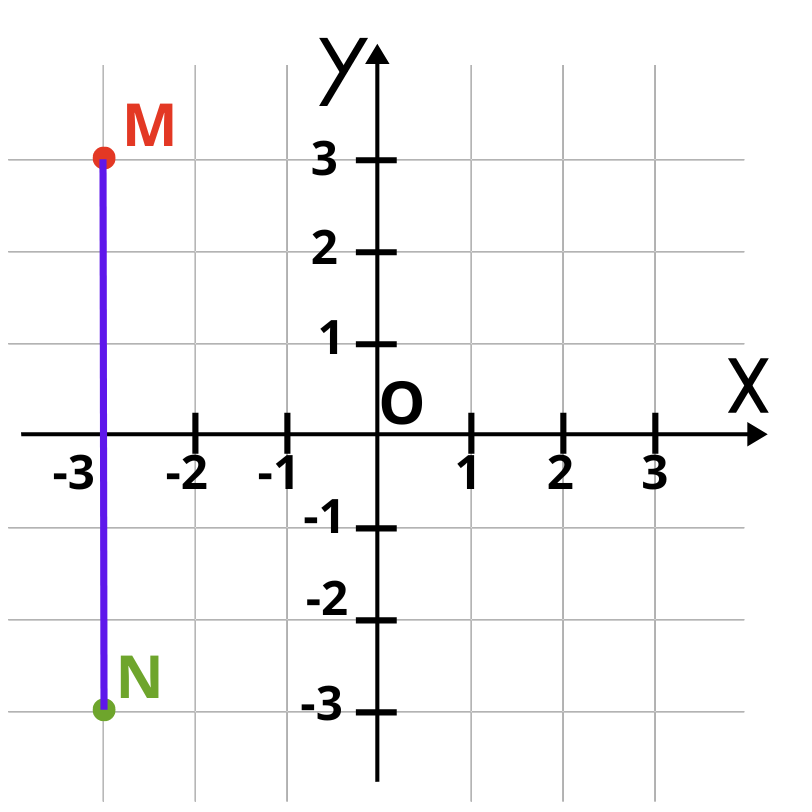
Точките M и N са симетрични спрямо оста Ox. Абсцисите им са равни, а ординатите им са противоположни числа: M(—3;3), a N(—3; —3). Двете се намират на равни разстояние от оста Оx. Ако прегънем чертежа по оста на симетрия, двете точки напълно ще съвпаднат.

Две точки са симетрични спрямо ординатната ос, когато абсцисите им са противоположни числа, а ординатите им са равни. Двете точки са на равни разстояния от оста Oy и ако прегънем чертежа по тази ос, те ще съвпаднат. Хайде да видим две точки, симетрични спрямо ординатната ос:

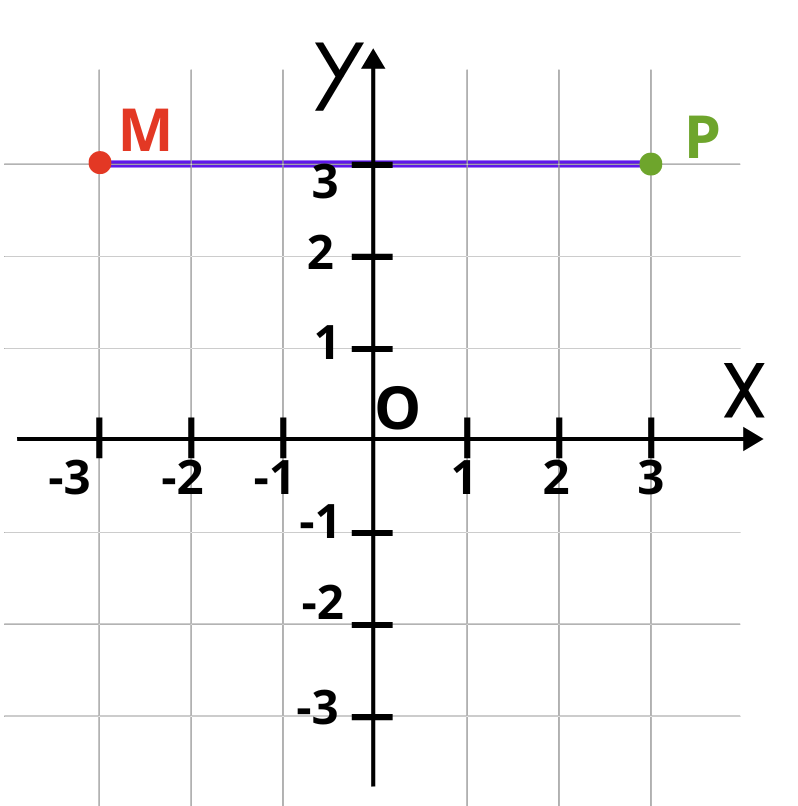
Точки M и P са симетрични спрямо оста Oy. Tехните координати са M(—3;3) и P (3;3).

Накрая да видим кои точки ще са симетрични спрямо ординатното начало.

Тук е още по-лесно, да видим две такива точки и веднага ще запомним как да ги разпознаваме!

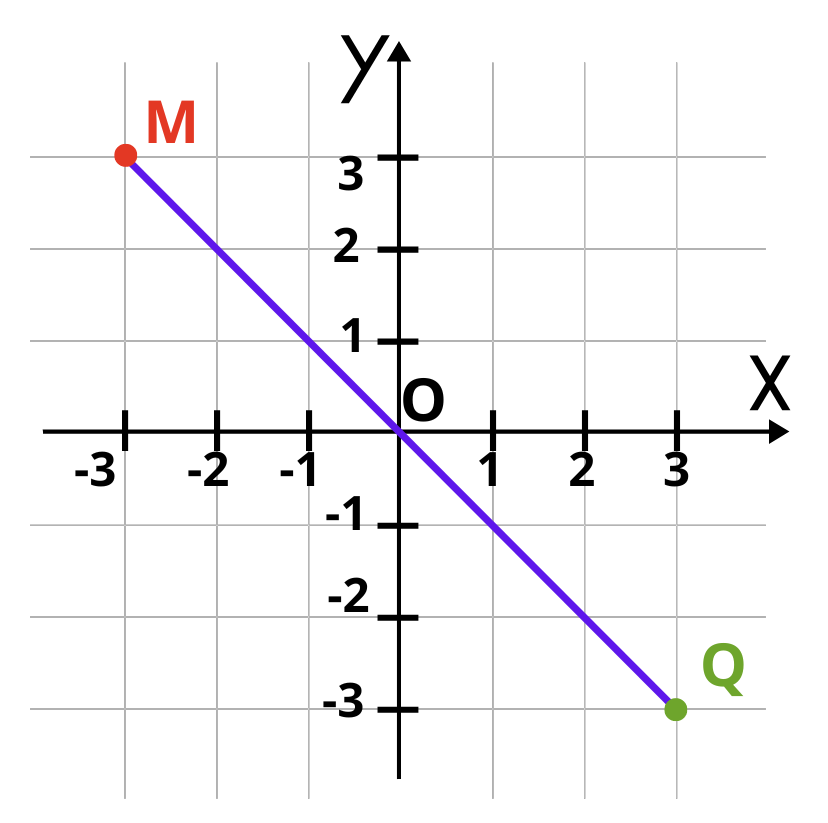
Нека запишем координатите на двете точки M(—3;3) и P (3;—3).

Забеля за ли, че двете абсциси и двете ординати са противоположни числа? Така може да разпознаваш точки, които са симетрични спрямо координатното начало. Ако свържеш двете точки с отсечка, тя ще мине през началото на координатната система и ще се получат две равни отсечки – OM и OQ.