Геометрични фигури в декартова координатна система
Здравейте, приятели! Време е да видим приложението на декартова координатна система в задачи с геометрични фигури. Ще се учим да ги построяваме по координатите на върховете им и да намираме тяхното лице.

Ако искаш да си припомниш какво представлява декартова координатна система, как се отчитат координати на точки и как се построяват симетрични точки, можеш да прочетеш ето тази статия:
Построяване на точка по зададени координати
Много е лесно да построим точка, когато знаем нейните координати.
Нека да построим точка M (—2; 1). Трябва да не забравяме, че първо се записва абсцисата на точката, а след това ординатата. Веднага се вижда, че т.М се намира във втори квадрант. За да ѝ намерим точното местоположение, трябва да вдигнем перпендикуляри от съответните стойности: —2 по оста Ox и 1 от оста Оy. Ето как ги построяваме последователно:
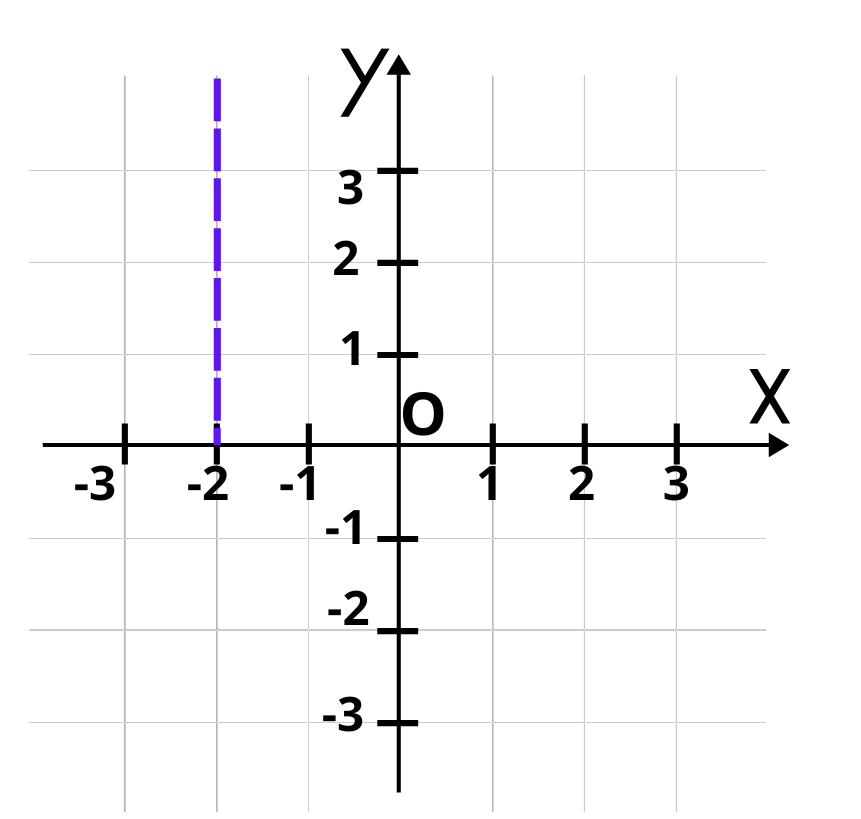
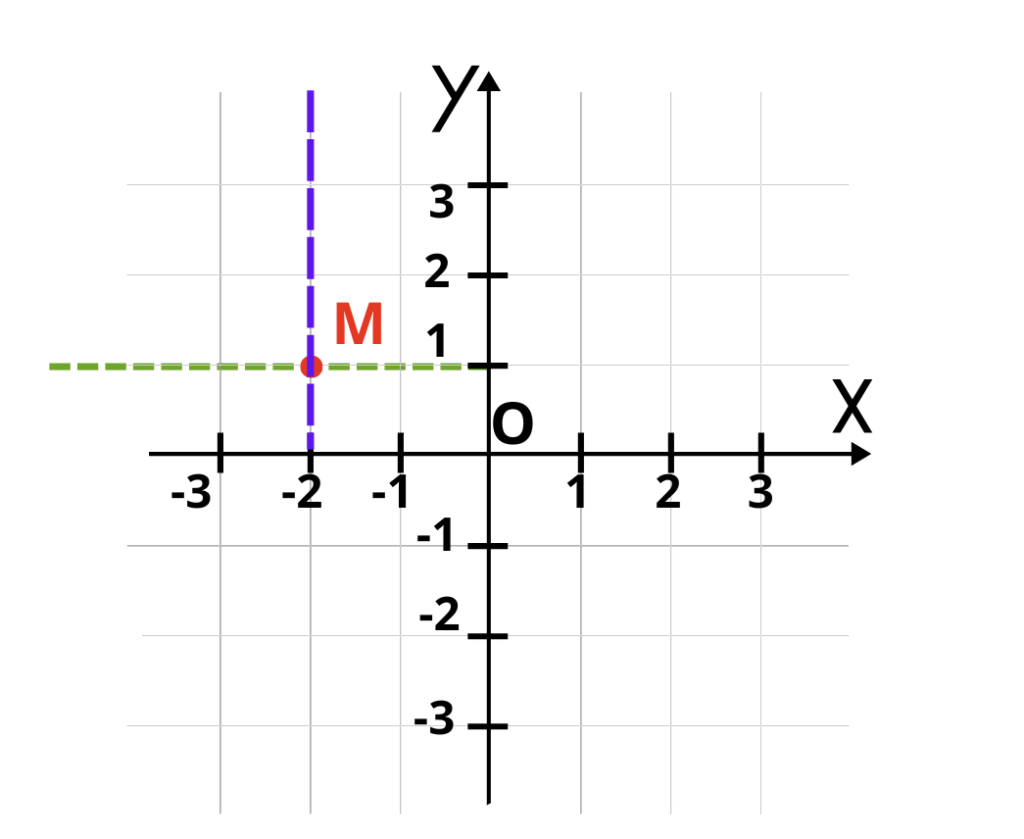
Точка М лежи на пресечната точка на двата перпендикуляра.
Лице на геометрични фигури в декартова координатна система
Едни от най-интересните задачи с декартова координатна система са тези, при които трябва да построим геометрична фигура и да пресметнем нейното лице.
Обикновено знаем точките от контура на фигурата или пък са ни дадени координатите на няколко от точките от контура, а останалите трябва да построим като използваме дадена зависимост.
Да видим една такава задача.

Намерете лицето на успоредника MNPQ, ако координатите на две от точките са: M(—2;3), N(3;3), точка P е симетрична на точка N спрямо координатното начало. Единичната отсечка на координатната система е 1 cm.
Първо трябва да построим двете точки, на които са дадени координатите:
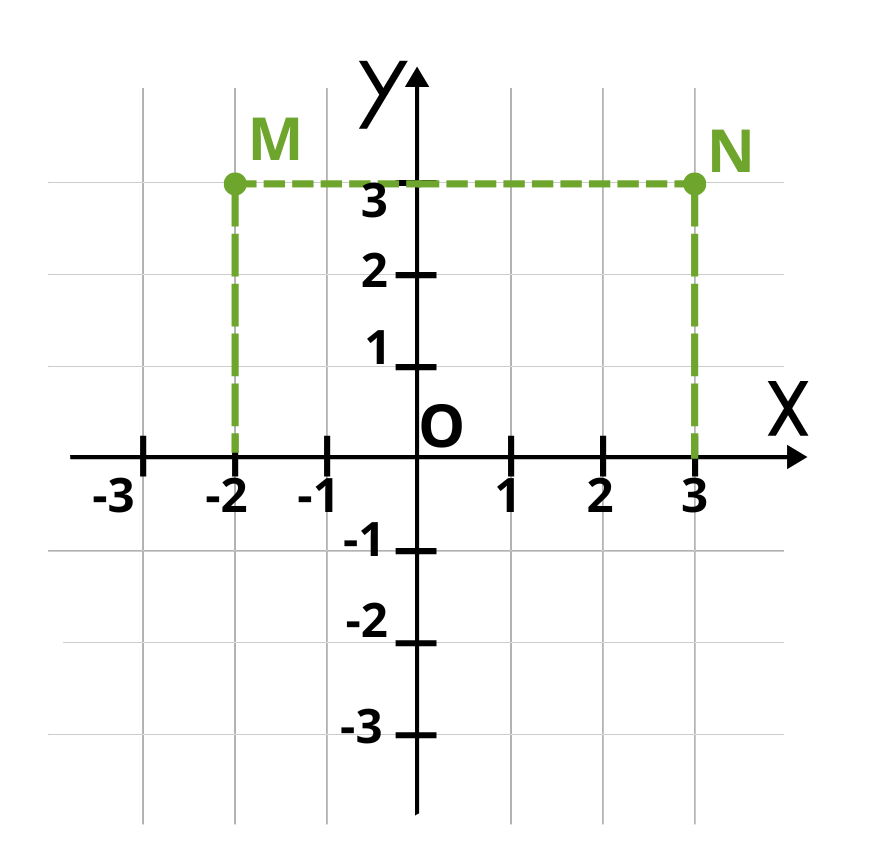
Сега трябва да построим точка P, която е симетрична на точка N спрямо координатното начало. Нейните координати трябва да са протовоположни числа на координатите на точка N. Ето ги и тях: P(—3;—3). Ако сме работили правилно, отсечката която свързва двете точки, трябва да минава през координатното начало. Да проверим:
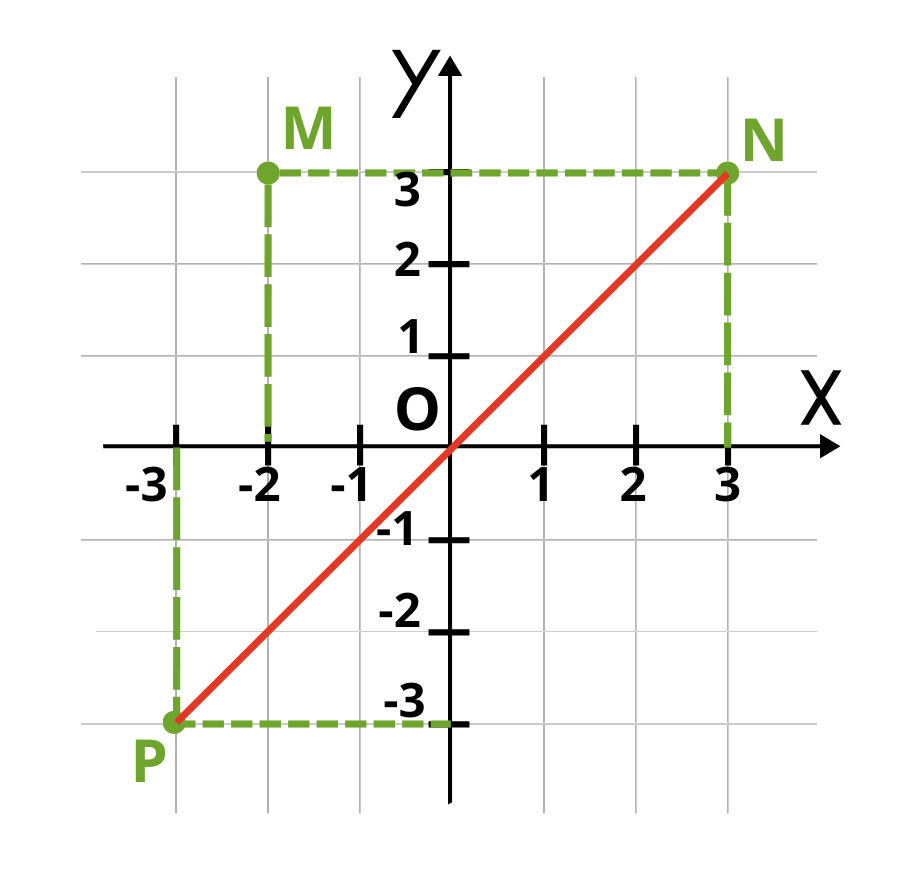
Остава да построим последния връх на успоредника. Първо да си припомним какво знаем за страните на този вид четириъгълник: срещуположните му страни са успоредни и равни.
Трябва да построим отсечка, равна и успоредна на MN. лесно се вижда, че дължината на MN e 5 cm. Тогава PQ също ще е 5 cm.
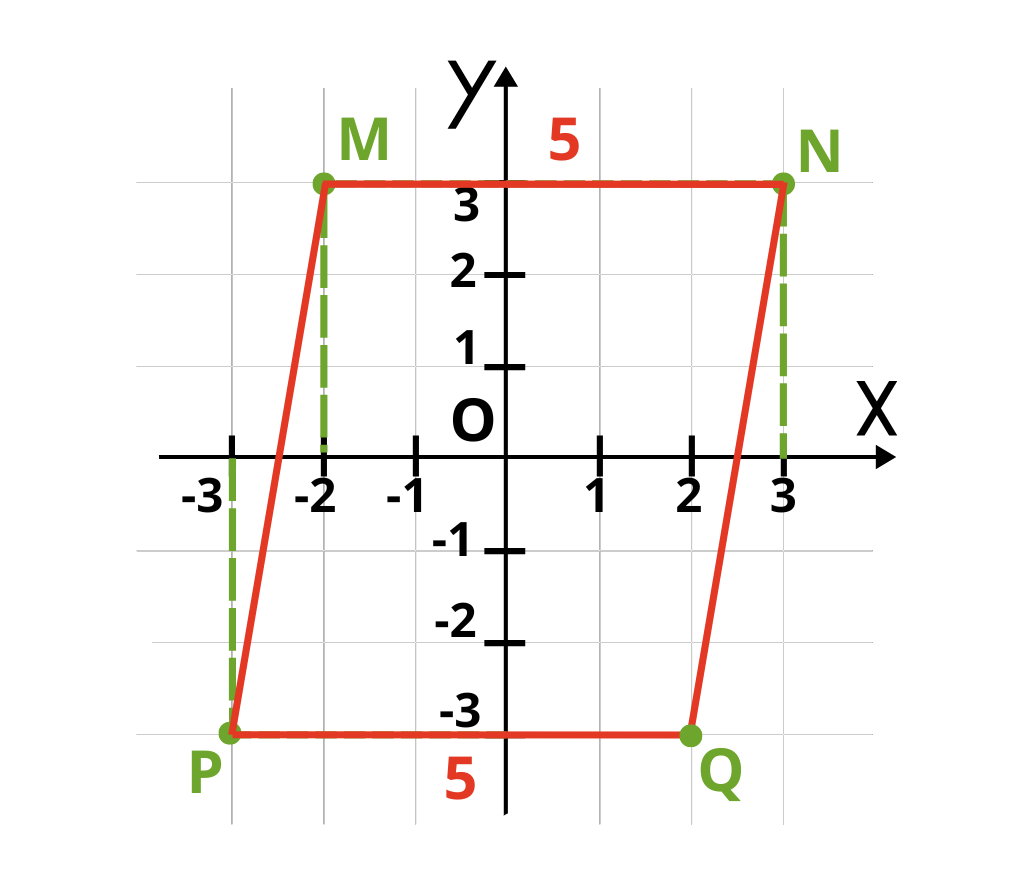
Точка Q е симетрична на точка M спрямо координатното начало. Вече е построен успоредника, остава да намерим лицето му. За целта ни трябва дължината на една страна и височината към нея. Можем да построим височината през всеки от четирите върха. Ето как изглежда през връх N към страната PQ:
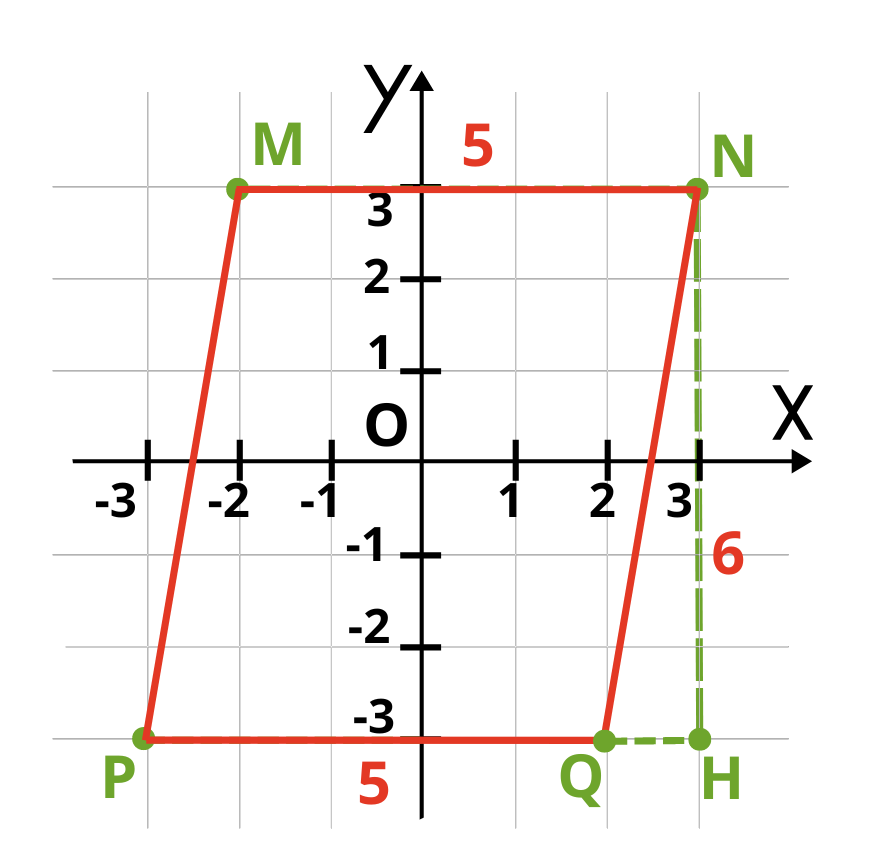
Височината NH e с дължина 6 cm. Записваме формулата за лице на успоредник и след това заместваме с нашите стойности:
SMNPQ = PQ.NH
SMNPQ = 5.6 = 30 cm2 задача с лице на триъгълник
Заплетена задача с лице на триъгълник
Време е за една задача, в която координатите на върховете на триъгълника са много заплетени. Да я видим!
Постройте триъгълник ABC в декартова координатна система с единична отсечка 1cm и намерете неговото лице, ако за върховете му е известно, че:
- т.A лежи на абсцисната ос и координатата ѝ по оста Ox е равна на стойността на израза: (—1/4).4/5+(—3,8)
- т.B e такава, че абсцисата ѝ е едноцифрено число, което е нито просто,нито съставно, а ординатата ѝ е равна на абсолютната стойност на израза: 2/7.(—7/4)+2,5
- т.С е с абсциса, равна на тази на т.B, а ординатата ѝ е най-голямото цяло число, по-малко от —2,9
Хайде да пресметнем координатите на трите върха:
Ординатата на точка А е равна на 0, тъй като тя лещи на абсцисната ос. Абсцисата на точка А определяме като пресметнем израза:
(—1/4).4/5+(—3,8) = —1/5—3,8 =
= —0,2—3,8 = —4
т.А е с координати (—4;0).
Абсцисата на точка е числото 1, а ординатата получаваме като пресметнем ето този модул:
I2/7.(—7/4)+2,5I = I—1/2+2,5I = I2I = 2
т.B е с координати (1;2).
Абсцисата на т.C e 1, а ординатата е равна на —3.
т.C е с координати (1;—3).
Сега можем да построим триъгълника.
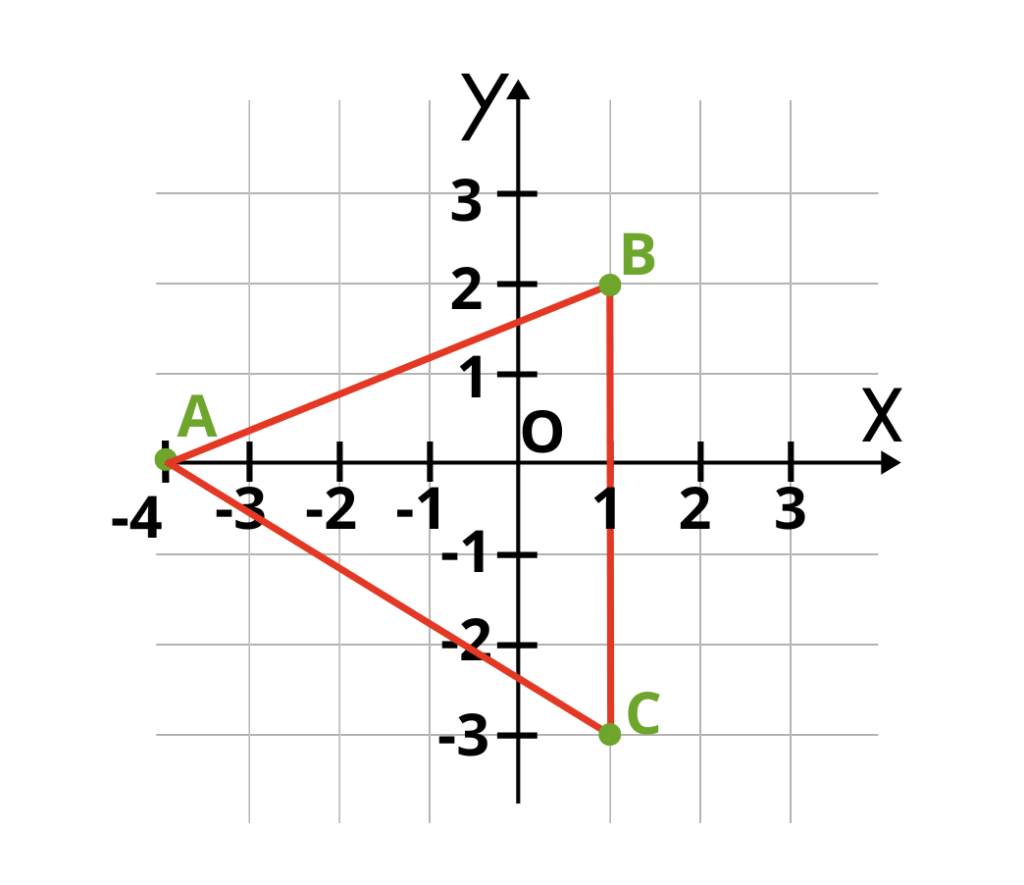
За да намерим лицето му е достатъчно да намерим дължината на една страна и височината към нея. Можем да определим дължината на страната BC като преброим единичните отсечки, BC = 5 cm. Височината към нея също се определя много лесно, тъй като перпендикулярът, спуснат от върха A съвпада с абсцисната ос.
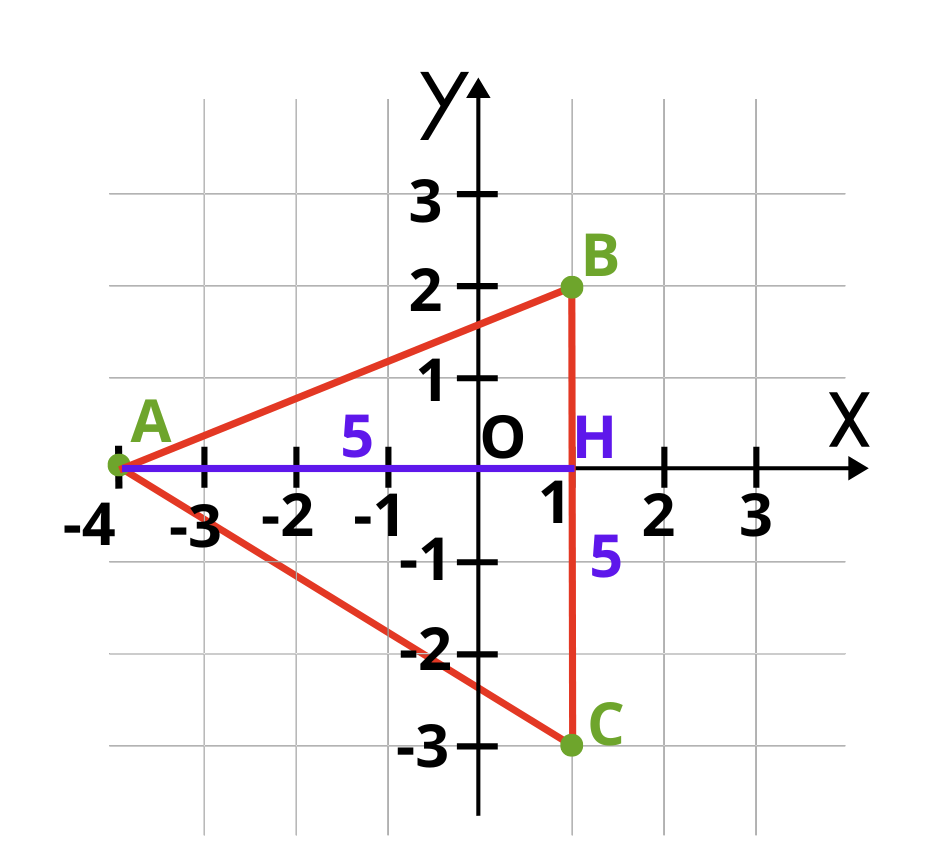
Височината AH е с дължина пет единични отсечки, AH = 5 cm.
И накрая намираме лицето на триъгълника
SABC = (BC.AH)/2
SABC = (5.5)/2 = 12,5 cm2

Време е да се упражниш със следващия тест!