Броене на правоъгълници
Здравейте, приятели на състезателната математика!

Време е да се запознаем с една много важна тема- броене на правоъгълници! Сигурен съм, че си я срещал както в учебниците по математика, така и на състезания. Сега ще разгледаме най-важните неща, които ще са ти ползени за тези задачи!
Какви фигури са правоъгълниците?
Първо трябва да се научим да различаваме правоъгълниците. Може би това ти се струва твърде елементарно, но всъщност често се случва объркване.

Коя от двете фигури е правоъгълник?
Сигурен съм, че повечето от вас ще ми отговорят, че това е сивата фигура, а зелената е квадрат. Всъщност и двете фигури са правоъгълници!
Квадратът е вид правоъгълник, на който са равни четирите страни.
Не можем да кажем обаче, че правоъгълникът е квадрат!
Стандартен начин за броене на правоъгълници

Ето една много лесна задача, за да видим как досега си решавал задачи с броене на правоъгълници.
Да разбием задачата на стъпки! Първо преборяваме единичните правоъгълници, които в случая са квадрати.
Имаме 4 квадрата- син, червен, лилав и жълт.
Сега да видим колко правоъгълника можем да образуваме от двойка квадрати:
син+червен квдрат;
лилав+жълт квадрат;
син+лилав квадрат;
червен+жълт квадрат;
Общо станаха четири правоъгълника, образувани от двойки квадрати.
Остана единствено големият квадрат, който е образуван от четирите малки квадрата.
Сумираме бройките: 4+4+1=9 правоъгълника!
Броене на правоъгълници, когато фигурите са много на брой
Стандартният начин за броене на правоъгълници е удобен, когато фигурите са малко. Ако обаче имаме да броим много повече правоъгълници, тогава е по-удобно да използваме друг начин. Сега ще ти го покажа със същата фигура, за да проверим дали работи!
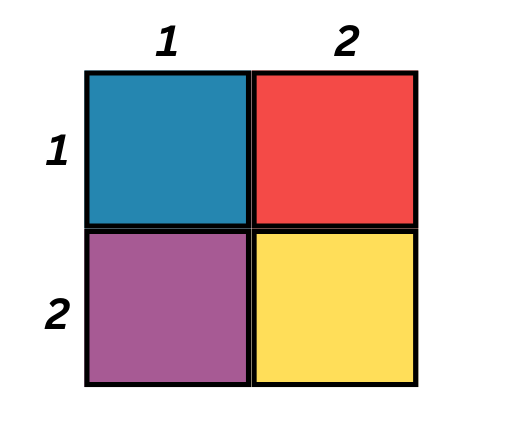
При този метод последователно записваме номер на всеки правоъгълник по дължина и широчина. После пресмятаме сборовете на числата по дължина и широчина.
Хайде да смятаме сборовете. Имаме едни и същи числа по дължина и широчина, така че получаваме:
1+2=3 сбор по дължина
1+2=3 сбор по широчина
Накрая умножаваме двата сбора: 3.3=9

Получихме един и същи брой правоъгълници и по двата метода! Хайде да видим още задачи!
Задача с броене на повече на брой правоъгълници
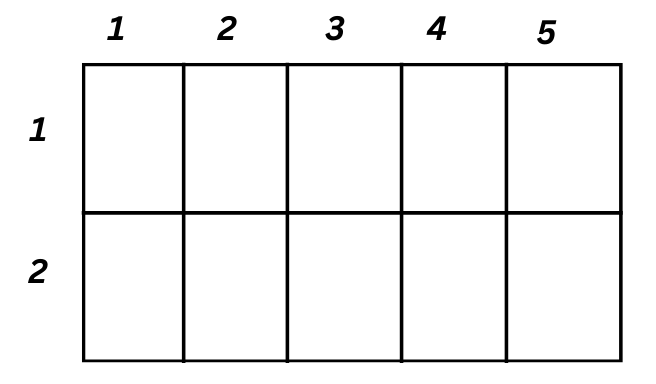
Да разгледаме ето тази схема с правоъгълници!
Тук ще използваме втория метод, за да спестим време. За целта номерираме всички правоъгълници по дължина и широчина.
Време е да пресметнем двата сбора:
1+2+3+4+5=15 сбор по дължина
1+2=3 сбор по широчина
А сега да пресметнем произведението на сборовете: 15.3=45

Представяш ли си, ако трябва да използваш стандартния начин за броене? Колко работа ще се падне и има шанс да пропуснем някой правоъгълник.
Задача, в която трябва да разделим схемата на няколко правоъгълника
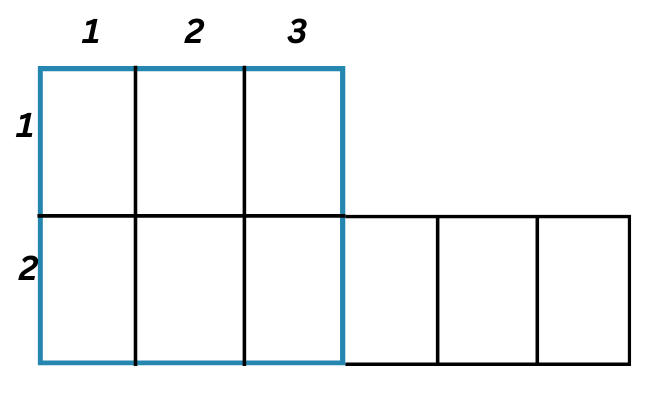
При тази задача трябва да подходим практично и да разделим нашата фигура на няколко правоъгълника. Първо отделяме един син правоъгълник и отново номерираме.
1+2+3=6 сбор по дължина
1+2=3 сбор по широчина
Произведението на двата сбора е 6.3=18
В синия правоъгълник попадат 18 правоъгълника!
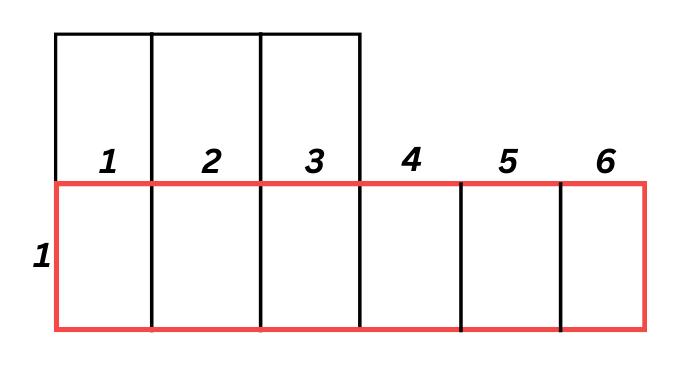
Да преброим сега фигурите в червения правоъгълник.
1+2+3+4+5+6=21 сбор по дължина
1 правоъгълник по широчина
Произведението на двете числа е 21.1=21
В червения правоъгълник попадат точно 21 правоъгълника.

Забеляза ли, че има няколко правоъгълника, които пападат както в синия, така и в червения правоъгълник?
Трябва да ги извадим от общият брой на всички правоъгълници. Оградени са с лилава линия на чертежа.
Първо номерираме правоъгълниците и след това намираме сборовете.
1+2+3=6 правоъгълника по дължина
1 правоъгълник по широчина
Произведението е 6.1=6
Броят на правоъгълниците в лилавата зона е 6!

Остана да съберем броя на правоъгълниците от червения и синия правоъгълник и да извадим тези от лилавия, защото те участват както в синия, така и в червения правоъгълник.
Накрая получаваме: 18+21-6=39-6=33 правоъгълника.
Трябва да бъдеш внимателен, когато имаш неправилна форма на цялата фигура с правоъгълници. Важно е да я разделиш на няколко отделни фигури, но след това да видиш кои правоъгълници се намират в повече от една фигура.
Харесаха ли ти задачите? Ако искаш да се упражниш още, можеш да решиш теста!