Абсолютна стойност (модул) на рационални числа
Днешният урок е за едно много важно математическо понятие, което ще ни помага да сравняваме рационални числа, да извършваме действия с тях, да пресмятаме стойност на по-интересни изрази. Това понятие е “абсолютна стойност” или както още се нарича-“модул” на рационално число.

За да разберем значението на това ново математическо понятие, трябва да можем да изобразяваме рационални числа върху числова ос. Ако това те затруднява, можеш да си припомниш нашата статия:
Рационални числа. Изобразяване на рационални числа върху числова ос.
Противоположни числа
Противоположните числа наричаме тези, които се различават само по знака си! Толкова е простичко!
Ето няколко примера за противоположни числа:
—2 и 2
—7,8 и 7,8;
3,785 и —3,785
2 1/4 и —2,25
Противоположното число на 0 и 0.
Забеляза ли нещо интересно в предпоследния пример? Всъщност 2 1/4=2,25.
Хайде да видим как се изобразяват противоположните числа върху числовата ос:
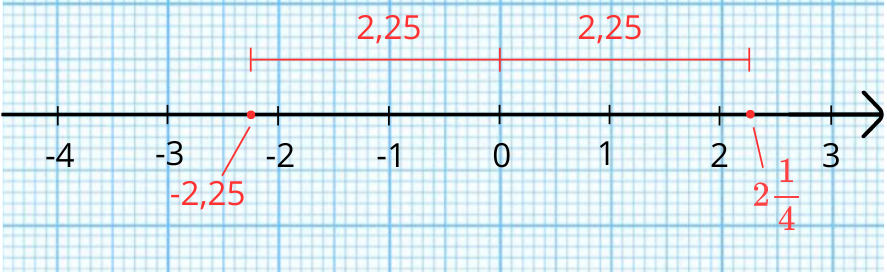
Ако приемем, че единичната отсечка е 1 cm, то двете числа —2,25 и 2 1/4 се изобразяват на 2,25 cm от началото на оста ( от числото 0). Предполагам се сещаш, че 25 стотни се намират точно по средата между 2 десети и 3 десети т.е. между втория и третия милиметър.
Готови сме да направим един много важен извод!
Противоположните числа се изобразяват на равни разстояния от началото на числовата ос!
Абсолютна стойност (модул) на рационално число
Зад тези думички се крие нещо много, много простичко! Абсолютната стойност на едно рационално число е равна на разстоянието от образа на числото върху числовата ос до началото на оста (до числото нула).
Има специални скоби, с които записваме абсолютната стойност- прави или модулни скоби. Ето ги и тях: I8I
Четем: модул на 8.
Да разгледаме как са разположени числата 3 и —3 на числовата ос и да помислим на колко ще са равни техните абсолютни стойности.
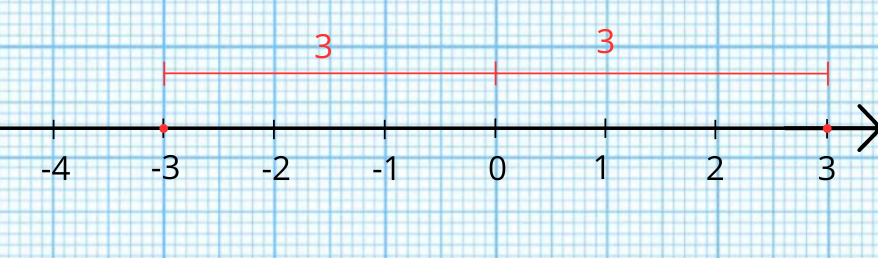
Разстоянието на числото 3 до нулата е 3 единични отсечки. Затова абсолютната стойност на числото 3 е 3. Ето как се записва:
I3I=3
Можем да го прочетем и като модулът на 3 е 3.
Модулът на числото —3 е също 3, тъй като се намира на 3 единични отсечки от началото на числовата ос.
Записваме I—3I=3.
Понеже разстоянието до нулата може да е само положително число или 0, тогава модулът на рационално число не може да е отрицателно число.
Модулът на числото 0 е 0, защото съвпада с началото на числовата ос, спрямо което отмерваме разстояние. Записваме I0I=0.

Модулът на всяко положително число е самото число!
Модулът на всяко отрицателно число е неговото противоположно число!
Пресмятане на изрази с абсолютна стойност
Да видим как изглежда един израз с абсолютни стойности и да опитаме да пресметнем стойността му:
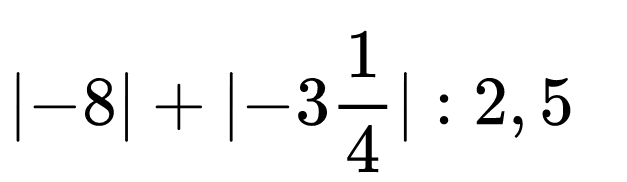
Първата ни работа е да пресметнем модулите на числата, останалата част от израза не променяме.
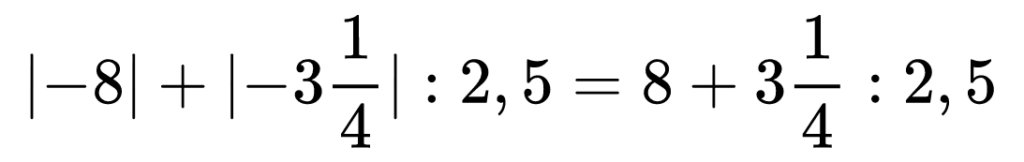
След това внимаваме за редът на действие. Първо извършваме делението, а след това пресмятаме сбора.
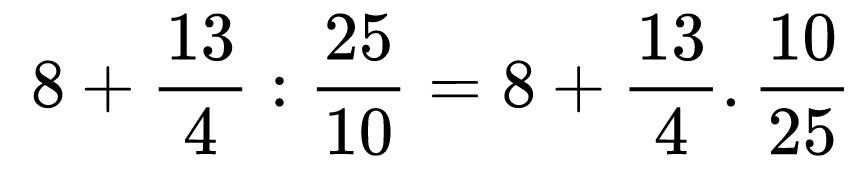
При изчисленията може да изберем да работим с обикновени или десетични дроби. Единственото ни ограничение е в случай, че в израза имаме периодична десетична дроб или получим такава при изчисленията (например 1/3, 2/3). Тогава трябва да пресмятаме с обикновени дроби.
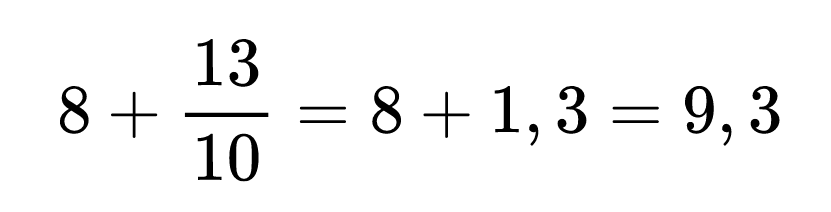
Отговорът също можем да запишем с десетична дроб или смесено число.
По-сложни изрази с абсолютна стойности
Изразите с модули могат да са още по-интересни!
Например в модулните скоби да има още едни модулни скоби!
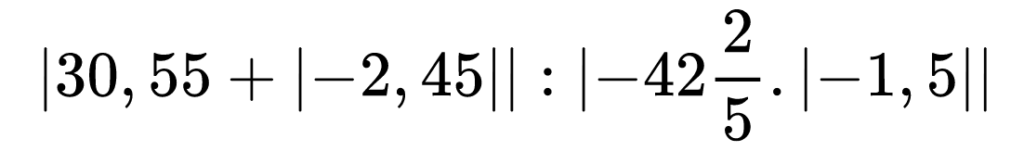
Първо пресмятаме вътрешните абсолютни стойности. Също както при изрази с вътрешни скоби, започваме действията от тях.
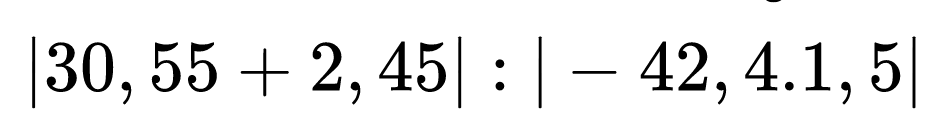
Забеляза ли, че този път превърнахме смесеното число —42 2/5 в десетичната дроб —42,4 ?
Сега можем да извършим действията във външните модулни скоби, след което да се освободим и от тях, като запишем абсолютните стойности на получените числа.
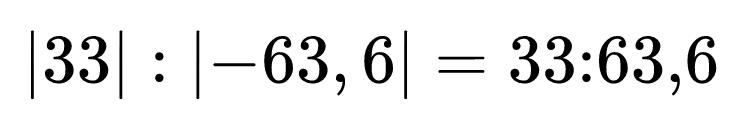
Накрая остава да пресметнем частното на двете числа. Удобно е да заменим знакът за деление с дробна черта и след това да умножим с 10 делимото и делителя. Така получаваме обикновена дроб, която съкращаваме до получаване на несъкратима обикновена дроб.
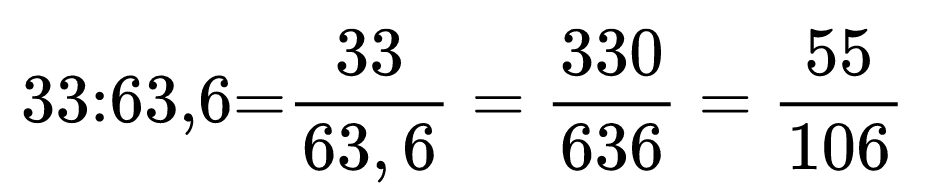

Абсолютната стойност на числата е много, много важна! Затова е добре да се упражниш със следващия тест!