Куб. Елементи. Развивка. Лице на повърхнина и обем на куб.
Замисляли ли сте се каква форма имат игралните зарове, шоколадчетата в кутия или строителните блокчета? Те са кубове – фигури, които се срещат навсякъде около нас. Всяко тяхно лице е перфектен квадрат, а разгърнати, те се превръщат в забавни мозайки. Днес ще влезем в ролята на изследователи на куба, ще разберем неговите тайни и ще видим как го използваме в реалния живот. Пригответе се за едно занимателно пътешествие в света на геометрията!
1. Теоретична част
1.1. Какво е куб?


Кубът е геометрично тяло с:
- 6 равни квадратни стени;
- 12 ръба, които свързват стените;
- 8 върха, където се срещат ръбовете;

Всеки ръб на куба е с една и съща дължина, която наричаме дължина на ръба: a.
Дължината на ръба се нарича измерение на куба.
1.2. Елементи на куба

- Срещуположни стени– ABCD и A1B1C1D1, ABB1A1 и DCC1D1, BCC1B1 и ADD1A1;
- Съседни стени– имат общ ръб;
- Ръбове – Кубът има 12 ръба. На чертежа това са: AB, BC, CD, DA, AA1, BB1, CC1, DD1, A1B1, B1C1, C1D1, D1A1;
- Върхове – Кубът има 8 върха. На нашия чертеж това са: A, B, C, D, A1, B1, C1, D1;
- Кубът се означава: ABCDA1B1C1D1

Всички ръбове на куба са равни.
Стените на куба са квадрати с равни страни.
Сборът от дължините на ръбовете на куба е равен на 12 . a, където a е дължината на ръба, а 12 е броят на ръбовете.
1.3. Развивка на куб

Ако „разгънем“ куба, всяко лице ще се превърне в квадрат, и те ще образуват плоска фигура – развивка. Развивката може да има различни форми, но винаги съдържа шест квадрата, свързани по ръбовете си.
Кубът има различни по форма разгъвки.

2. Лице на повърхнина на куб


Развивката на куба е фигура, която се състои от 6 квадрата. От изученото до четвърти клас, по математика, знаем, че лицето на квадрат се изчислява по формулата:
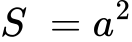
Следователно лицето на развивката на куба може да бъде изразено като:
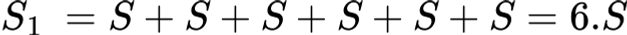

Сборът от лицата на стените на куба се нарича лице на повърхнината на куба: S1.

Вече казахме, че за квадрат със страна a: S = a2. Следователно за куб с ръб a, лицето на повърхнината ще бъде равно на:

Пример: Ако ръбът на куб е a = 3 cm, тогава лицето на повърхнината му е:
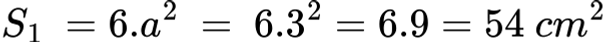
3. Обем на куб

Обем е количественият израз на това каква част от пространството заемат обектите (телата).Едномерните обекти (например линия) и двумерните обекти (например квадрат) имат нулев обем в триизмерното пространство. Мерната единица за обем в Международната система единици (SI) е кубически метър и се означава с m3.

Числото, което показва колко пъти един куб се “побира” в разглеждано тяло, се нарича обем на тялото и се означава с латинската буква V.

Обемите на телата могат да се измерват като се използват единични кубове с ръб, който е с дължина 1mm, 1 cm, 1 dm или 1 m.

Трябва да запомним обаче, че когато мерим течности използваме специална мярка: литър (L). В тези случаи, вместо да използваме терминът обем, казваме, че намираме вместимостта на съдовете, в които е течността (кана, шише, цистерна, басейн и др.).

Ако даден куб има ръб a, то неговия обем V е равен на:

Пример: Ако ръбът на куба е a = 4 cm тогава неговият обем ще бъде:

4. Задачи
- Подаръчна кутия
Подаръчна кутия с форма на куб има ръб, дълъг 5 cm.

- Какъв е обемът на кутията?
- Каквo е лицето на цялата ѝ повърхност?
Дадено:
aкуб = 5 cm;
Решение:
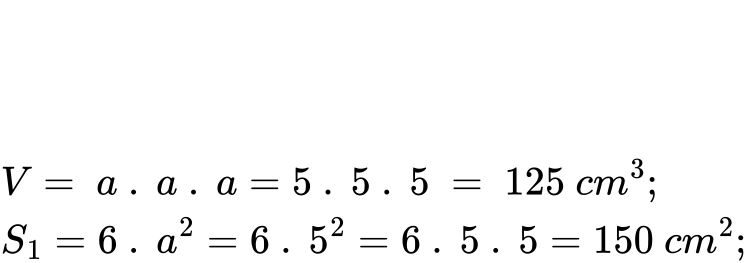
Отговор:
- Обемът на кутията е 125 cm3.
- Площта на повърхността е 150 cm2.
2. Развивка на куб
Имате развивка на куб, изрязана от хартия с квадратни страни по 8 cm.

- Каква е площта на хартията?
- Ако сглобите куба, какъв ще бъде обемът му?
Дадено:
aкуб = 8 cm;
Решение:

Отговор:
- Площта на хартията е 384 cm2.
- Обемът на куба е 512 cm3.
5. Практически задачи

- Създаване на модел на куб
- Вземете лист картон. Начертайте развивка на куб (шест квадрата, всеки със страна 5 cm).
- Изрежете я и я сглобете в триизмерна форма с лепило или тиксо.
- Изследване на обем и площ
- Създайте куб с различна дължина на ръбовете 2 cm,3 cm,4 cm.
- Измерете площта на повърхнината и обема му. Сравнете резултатите.
6. Заключение
След като вече знаете всичко за куба – неговите елементи, развивката и свойствата му, погледнете около себе си. Ще го откриете в играчки, мебели, опаковки и още много други неща. Кубът е не само математическа фигура, но и част от нашия свят. Следващия път, когато сглобявате кутия за подарък или играете с кубчета, спомнете си – в тези малки форми се крият големи тайни на пространството!







